Target: 本文提出一種根據屬性生成圖像的産生式模型 。
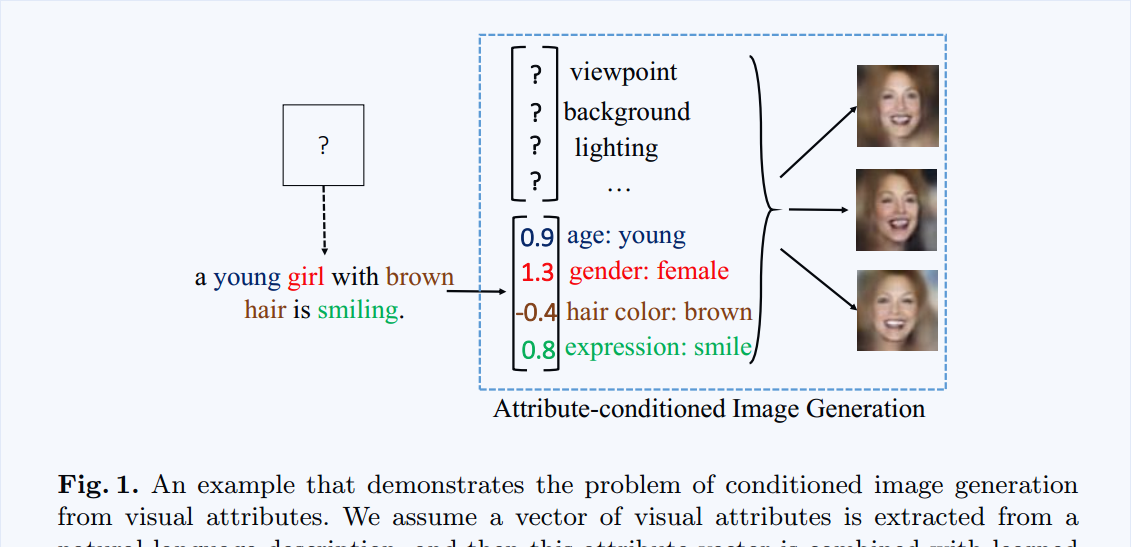
有了具體屬性的協助,生成的圖像更加真實,降低了采樣的不确定性。
基于這個假設,本文提出一種學習架構,得到了基于屬性的産生式模型。
1. Attribute-conditioned Generative Modeling of Images.
3.1 Base Model: Conditional Variational Auto-Encoder (CVAE)
關于該節,可以參考博文:http://www.cnblogs.com/wangxiaocvpr/p/6231019.html
給定屬性 y 和 latent variable z, 我們的目标是建構一個模型,可以在條件 y 和 z 的基礎上産生真實的圖像。此處,我們将 $p_\theta$ 看作是一個産生器,參數為 $\theta$。
條件式圖像産生是簡單的兩部操作,如下:
1. 随機的從先驗分布 p(z) 中采樣出 latent variable z;
2. 給定 y 和 z 作為條件變量,從 $p_\theta (x|y, z)$ 産生圖像 x。
此處,學習的目标是找到最佳的參數 $\theta$ 可以最大化 log-likelihood $log p_\theta (x|y)$. VAE 試着去最大化 log-likelihood 的 variational lower bound。特别的,一個輔助的分布 q 被引入來估計真實的後驗機率。
此處,the prior $p_\theta (z)$ 被認為是服從 各項同性的多方差高斯分布(isotropic multivariate Gaussian distribution),兩個條件分布 p 和 q 是多方差高斯分布。我們将輔助的 proposal distribution q 看作是 recognition model,條件資料分布 p 是 generation model。
上述模型的第一項 KL(q|p)是一個正則化項,目标是減少 the prior p(z) 和 the proposal distribution q 之間的差距,第二項是樣本的 log likelihood。
實際上,我們通常考慮 a deterministic generation function 給定 z 和 y 的條件分布 $p_{\theta}(x|z,y)$ 的均值 $x = \mu_{\theta}(z, y)$ 。是以,标準的偏差函數 $\delta_\theta(z, y)$ 是一個固定的常量,并被所有像素點共享,因為 latent factors 捕獲了所有的 data variation。是以,我們可以将第二項改寫為 重構誤差 L(*,*)(即:l2 loss):
3.2. Disentangling CVAE with a Layered Representation.
一張圖像可以看做是一個 foreground layer 和 background layer 的組合,如下:
其中,圓圈符号表示元素級相乘(element-wise product)。g 是 an occlusion layer or a gating function 決定背景像素點的可見性,1-g 表示了前景像素點的可見性。
但是基于上述公式的 model 可能受到 錯誤預測的 mask 的幹擾,因為 it gates the foreground region with imperfect mask estimation.
我們預測下面的函數,該函數對 mask的預測誤差更加魯邦:
當照明條件穩定的時候,以及背景在一定的距離,我們放心的假設: foreground and background pixels 是從互相獨立的 latent factors.
為了這個目标,我們提出一種分離的表達(a disentangled representation) 在 latent space 的,z = [zF, zB]。zF 和 屬性 y 一起捕獲了 the foreground factors,而 zB 捕獲了 the background factors. 是以,對應的,the foreground layer xF 是從 $\mu_{\theta F}(y, z_F)$ 中産生的,而 the background layer xB 從 $\mu_{\theta F}(z_B)$ 中産生的。前景的形狀和位置決定了背景遮擋,是以,
the gating layer g 是從 s 産生的。其中 the last layer of s(*) 是 sigmoid function。
總的來說,我們按照下面的過程來進行 the layered generation process:
1. 采樣前景和背景隐層變量zF, zB ;
2. 給定 y 和 zF, 産生前景層 xF 和 gating layer g; 以及 背景layer。
3. 合成一張圖像 x 。
Learning 。以完全無監督的方式學習我們的 layered generative model 是非常有挑戰的。我們僅僅從圖像 x infer 關于 xF, xB and g.
本文中,我們進一步的假設 the foreground layer xF (as well as the gating variable g) 在訓練的過程中,是可見的。我們訓練一個模型,最大化 the joint log-likelihood $log p_\theta (x, xF, g|y)$ 而不是 $log p\theta(x|y)$。有了解綁的 latent variable zF 和 zB,我們 infer layered model a disentangleing conditional variational auto-encoder (disCVAE)。我們對比了 the graphical models of disCVAE with vanilla CVAE in Figure 2.
基于 the layered generation process, 我們将 産生式模型 (the generation model) 寫成下面的方式:
而 判别式模型 (the recogniton model)記為:
the variational lower bound $L_{disCVAE}$ 記為:
4. Posterior Inference via Optimization.
一旦 the attribute-conditioned generative model 訓練完成後,給定屬性 y 和 latent variable z 後,圖像 x 的 the inference 或者 generation 是非常直覺的。
但是,給定 an image x,latent variable z 的 inference 及其對應的屬性 y 是未知的。實際上,the latent variable inference 是非常有用的,因為其確定了在新圖像上的 model evaluation。
首先,我們注意到:the recognition model q may not be directly used to infer z.
一方面,作為估計,我們不知道其距離真實的 posterior p 有多遠。因為在 variational learning object 中,KL divergence 被扔掉了;
另一方面,這種估計在其他模型,如:GANs,甚至不存在。
我們給出了一種 general approach 進行 posterior inference,在 latent space 進行 optimization:
注意到,the generation models or likelihood terms 可以是 non-Gaussian or even a deterministic function with no proper probabilistic definiton.
是以,為了使得我們的算法更加 general,我們将上述的 inference 的過程,寫成下面能量最小化的問題:
其中,L 是圖像重構的 loss,R 是 先驗正則化項。以簡單的高斯model 作為例子,the posterior inference 可以重新寫作:
注意到,我們用 the mean function u 為 a general image generation function。因為 u 是一個複雜的神經網絡,優化 公式(9)本質上是誤差回傳,我們利用 ADAM method 來求解。
本文與最新提出的 神經網絡可視化 和 文本合成算法 的差別在于:
We use generation models for recogniton; while others use recogniton model for generation.
實驗部分: