第一部分:定義
樹(Tree)是n(n>=0)個結點的有限集。 n = 0 時成為空樹。在任意一顆非空樹中:
(1). 有且僅有一個特定的成為根(root)的節點。
(2). 當 n > 1 時,其餘結點可以分為m個互不相交的有限集 T1、 T2、 T3 .....Tm,其中每一個集本身又是一棵樹,并且稱為根的子樹。
第二部分:基本概念
1. 結點分類
在一棵樹中,結點分為 根結點、内部結點和葉結點(又稱終端結點)。
結點擁有的子樹的數目稱為結點的度(Degree)。 B的度為1, D的度為3
在一棵樹中, 最大的結點的度為樹的度。 由于D的度最多,是以樹的度就是3.
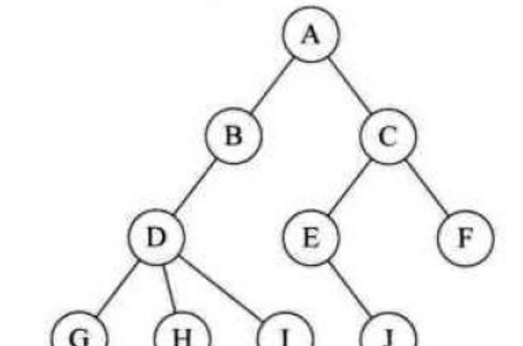
2.節點間關系
其中B是A的孩子, A是B的雙親, C是B的兄弟。 之是以稱之為雙親是因為對于結點來說父母同體,隻有這麼稱呼是比較合适的了。
3. 其他相關概念
結點的層次: 從根開始算起, 根為第一層,然後第二層,第三層....
樹的深度或高度: 結點的最大層次就是樹的深度或高度。
有序樹:如果将樹中結點的各子樹看成是從左到右有次序的,不能互換的,那麼該樹就是有序樹,否則就是無序樹。
第三部分: 樹的存儲結構
我們知道, 樹中某個結點的孩子有多個,是以無論是使用順序存儲結構還是使用鍊式存儲結構,都不能很好的表示樹。但是我們可以利用順序存儲結構和鍊式犓結構的特點來實作之。
一. 雙親表示法
我們假設以一組連續的空間存儲樹的結構,同時在每個節點中,附加一個訓示器訓示其雙親結點在數組中的位置,也就是說,每個結點不僅僅知道自己是誰意外,還知道它的雙親在數組中的哪個位置。
即一個結點包含兩個部分: 1. data(資料域) --- 用于存儲結點的資料資訊。 2. parent (指針域) --- 用于存儲該結點的雙親在數組中的下标。
注意: 這樣的好處是我們可以根據結點的parent指針很容易的找出它的雙親結點,是以複雜度是O(1), 但是如果我們要知道結點的孩子是誰,就得周遊整個結構才行。為了解決這個問題,我們可以增加一個結點最左邊孩子的域,可以稱之為長子域。 孩子可以找到了, 但是找兄弟呢 ? 我們還可以增加一個兄弟域,這樣,可以發現:
存儲結構的設計是一個非常靈活的過程,一個存儲結構設計的是否合理,取決于該存儲結構的運算是否合适、是否友善, 時間複雜度好不好等等。
二. 孩子表示法
如果一棵樹中的每一個結點都有很多的孩子, 那麼這時孩子為重, 我們就可以考慮每個結點有多個指針域, 每個指針域指向一顆子樹的根節點, 這種方法就是多重連結清單表示法。 不難想象,多重連結清單表示法的最終結構和一顆樹的結構是無異的。但是根據一個結點需要多少個域的不同,我們可以将多重連結清單表示法分為下面兩種:
1. 每個結點的指針域的個數是數的度
優點 這樣做的好處在于樹的結構是穩定的、整齊的、維護起來較為友善。 缺點 壞處在于有可能很多指針域都是空着的,造成了資源的浪費。
2. 每個結點的指針域的個數就是其子節點的個數(即它的度)
優點 這樣做的好處在于不會造成資源的浪費。 缺點 壞處在于這樣在後期維護起來會比較麻煩,且結構會比較混亂。
ok! 那有沒有一種方法可以回避上面的缺點呢? 當然有,這就是孩子表示法了, 孩子表示法,即以n個結點的單連結清單作為存儲結構, 則n個結點就有n個孩子連結清單,每個結點又會引出孩子的節點(如果沒有孩子,就不會引出,如果有,就一直引下去)。
這樣的表示法缺點在于,如果知道某個結點的雙親是誰呢? 并不難,隻要我們把雙親表示法和孩子表示法綜合一下不就行了嗎? 這種思路當然可行。
三、 孩子兄弟表示法
第四部分:二叉樹
二叉樹(Binary Tree)是n個結點的有限集合,該集合或者為空集,或者由一個根節點和兩顆互不相交的、分别稱為根節點的左子樹和右子樹的二叉樹組成。
1. 二叉樹的特點
- 每個結點最多有兩個子樹。
- 左子樹和右子樹的順組是不能随意颠倒的。
- 即使某個結點隻有一個子樹,也要厘清楚左子樹還是右子樹。
- 三個結點可以構成 5 種不同的二叉樹。
資料結構之樹
2. 一些特殊的二叉樹
- 斜樹 如上圖中的第二個圖和最後一個圖就是斜樹 --- 每一層都隻有一個結點,結點的個數和二叉樹的深度相同。
- 滿二叉樹 在一顆二叉樹中,如果所有分支結點都存在左子樹和右子樹,并且所有的葉子都在同一層上, 這樣的二叉樹就稱為滿二叉樹。
資料結構之樹 - 完全二叉樹 對于一顆具有n個結點的二叉樹按層序編号,如果編号為i (1 <= i <= n)的結點與同樣深度的滿二叉樹中編号為i的結點在樹中的位置完全相同,則這棵樹就是完全二叉樹。 編号方式: 從上到下,從左到右。
- 注意: 滿二叉樹一定是完全二叉樹, 完全二叉樹不一定是滿二叉樹。
3. 二叉樹的5條性質
性質一: 在二叉樹的第i層上最多有2i-1 個結點。(i>=1). 如二叉樹的第三層上最多有2 的 2 次方個結點。
性質二: 在深度(或高度)為k的二叉樹上最多有 2k - 1 個結點。 如深度為3的二叉樹的結點數最多為 2 3 - 1 = 7個結點。
性質三: 對于任意一顆二叉樹T, 如果其終端的節點數為n0 ,度為2的節點數為n2, 則有n0= n2 + 1;
性質四: 具有n個結點的完全二叉樹的深度為[log2n] + 1 (其中[x]表示不大于x的最大整數)。
性質五:
如果對一顆有n個結點的完全二叉樹(其深度為[log2n] + 1)的結點按層序編号(從上到下,從左到右), 對任一結點i (1 <= i <= n)都有:
1. 如果 i = 1, 那麼結點i是二叉樹的根。 如果i > 1, 那麼雙親是結點[i/2]。
2. 如果 2i>n, 則結點 i 無左孩子,否則其做孩子是2i。
3. 如果2i + 1 > n, 則結點i無右孩子, 否則其右孩子是結點 2i + 1;
第五部分:周遊二叉樹
二叉樹的周遊 ( traversing binary tree )是指從根節點出發, 按照某種次序依次通路二叉樹中的所有結點,使得每個結點都被通路一次且僅被通路一次。
這裡的兩個關鍵詞是 通路 和 次序。
顯然,二叉樹的通路次序不同于線性結構,對于線性結構而言,最多也就是從頭到尾、循環、雙向等簡單的周遊方式。樹的結點之間不存在唯一的前驅和後繼,是以在通路了一個結點之後,下一個被通路的結點面臨着不同的選擇。因而,對于二叉樹而言,周遊結點的方式就完全不同了。
說明:一般我們的習慣是從左到右的,這裡同樣也做出這樣的限制。那麼周遊時,前中後是指根節點被通路的時間上的前、中、後。
如前序周遊時先通路根節點、 中序曆時中間的時候通路根節點、後續周遊是最後通路根節點。 不論是哪種周遊方式都是先左子樹、後右子樹。
一: 前序周遊
規則: 若二叉樹為空, 則空操作傳回,否則先通路根結點,然後前序周遊左子樹,在前序周遊右子樹。
在二叉樹中,先根後左再右。巧記:根左右。
二: 中序周遊
規則: 若樹為空, 則空操作傳回, 否則先從根節點開始(注意并不是先通路根節點),中序周遊根節點的左子樹,然後是通路根節點,最後中序周遊右子樹。
在二叉樹中,先左後根再右。巧記:左根右。
注意: 對稱周遊就是中序周遊。
三: 後續周遊
規則: 若樹為空,則空操作傳回,否則從左到右先葉子結點的方式周遊通路左子樹,最後是通路根節點。
在二叉樹中,先左後右再根。巧記:左右根。
四:層序周遊
規則: 若樹為空,則空操作傳回,否則從樹的第一層開始,也就是根節點開始通路,從上而下逐層周遊,在同一層中,按照從左到右的順序對結點逐個通路。
這個是最為簡單的,隻要遵循從上到下、從左到右的規則即可。
規則: 1. 這裡的空操作傳回,就是指向上傳回,且空操作傳回是共同點。 2. 這裡的左子樹、右子樹和根節點都是相對的,環境和事件稍有改變,這些名詞所代表的實體就發生了徹底的變化。