樹:非線性結構——————其實更像是一串葡萄,哈哈
定義:
專業定義:
1、有且隻有一個成為根節點;
2、有若幹個互不相交的的子樹,這些子樹本身也是一顆樹;
通俗的定義:
1、樹是由節點和邊(指針域)組成;
2、每個節點隻有一個父節點,但可以有很多個子節點;
3、但有一個節點例外,該節點沒有父節點,此節點成為根節點;
涉及的術語:
節點, 父節點, 子節點, 子孫, 堂兄弟;
深度:從根節點到最底層節點的層數稱之為深度;
葉子節點:沒有子節點的節點
非終端節點:實際就是非葉子節點
度:子節點的個數;
樹的度:子節點的個數數目中最大值;
樹分類:
一般樹:任意一個子節點的個數的都不受限制;
二叉樹;任意一個節點的位元組點的個數最多兩個,且子節點的位置不可改變;
一般二叉樹
滿二叉樹:在不增加樹層數的前提下,無法再多添加一個節點的二叉樹;
完全二叉樹(重點):如果隻是删除了滿二叉樹最底層右邊的連續若幹個節點。這樣形成的二叉樹;
森林:n個互不相交的樹的集合;
二叉樹的存儲(重點):(一般二叉樹轉成完全二叉樹來存儲?原因是樹是非線性的,而我們要線性的儲存它,是以要将非線性轉成線性來存儲)
連續存儲【完全二叉樹】:
優點:查找某個節點的父節點和子節點(包括查找某個節點有沒有子節點)
缺點:耗用記憶體空間過大;
鍊式存儲:
(每個節點分三塊)
一般樹的存儲:
雙親表示法,孩子表示法,雙親孩子表示法,
二叉樹表示法:
把一個普通樹轉化成二叉樹來儲存,具體轉換方法:設法保證任意一個節點的左指針域指向它的第一個孩子,右指針域指向它的兄弟;
通過此辦法,就可以将一顆樹轉化為二叉樹;
· 一個普通樹轉化成的二叉樹一定沒有右子樹;
如下圖所示:
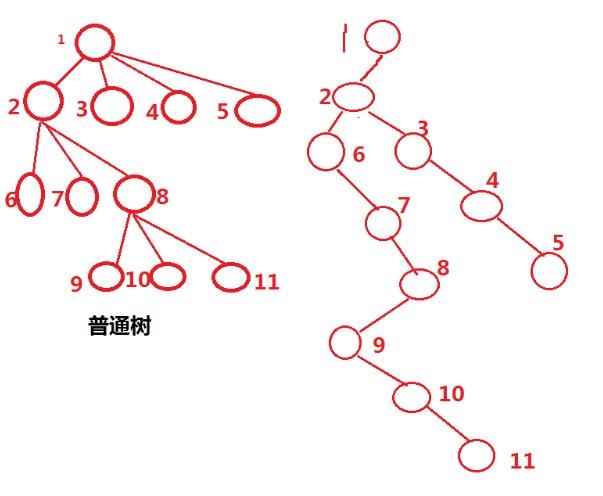
森林的存儲:
轉化為二叉樹儲存;規則如同普通樹轉化成二叉樹一緻;(每棵樹根節點為兄弟節點)
如下圖所示:
霍夫曼樹:每個節點要麼沒有子節點,要麼有兩個子節點;