前面一篇文章介紹了2-3查找樹,可以看到,2-3查找樹能保證在插入元素之後能保持樹的平衡狀态,最壞情況下即所有的子節點都是2-node,樹的高度為lgN,進而保證了最壞情況下的時間複雜度。但是2-3樹實作起來比較複雜,本文介紹一種簡單實作2-3樹的資料結構,即紅黑樹(Red-Black Tree)
定義
紅黑樹的主要是想對2-3查找樹進行編碼,尤其是對2-3查找樹中的3-nodes節點添加額外的資訊。紅黑樹中将節點之間的連結分為兩種不同類型,紅色連結,他用來連結兩個2-nodes節點來表示一個3-nodes節點。黑色連結用來連結普通的2-3節點。特别的,使用紅色連結的兩個2-nodes來表示一個3-nodes節點,并且向左傾斜,即一個2-node是另一個2-node的左子節點。這種做法的好處是查找的時候不用做任何修改,和普通的二叉查找樹相同。
根據以上描述,紅黑樹定義如下:
紅黑樹是一種具有紅色和黑色連結的平衡查找樹,同時滿足:
- 紅色節點向左傾斜
- 一個節點不可能有兩個紅色連結
- 整個樹完全黑色平衡,即從根節點到是以葉子結點的路徑上,黑色連結的個數都相同。
下圖可以看到紅黑樹其實是2-3樹的另外一種表現形式:如果我們将紅色的連線水準繪制,那麼他連結的兩個2-node節點就是2-3樹中的一個3-node節點了。
表示
我們可以在二叉查找樹的每一個節點上增加一個新的表示顔色的标記。該标記訓示該節點指向的節點的顔色。
private const bool RED = true;
private const bool BLACK = false;
private Node root;
class Node
{
public Node Left { get; set; }
public Node Right { get; set; }
public TKey Key { get; set; }
public TValue Value { get; set; }
public int Number { get; set; }
public bool Color { get; set; }
public Node(TKey key, TValue value,int number, bool color)
{
this.Key = key;
this.Value = value;
this.Number = number;
this.Color = color;
}
}
private bool IsRed(Node node)
{
if (node == null) return false;
return node.Color == RED;
}
實作
查找
紅黑樹是一種特殊的二叉查找樹,他的查找方法也和二叉查找樹一樣,不需要做太多更改。
但是由于紅黑樹比一般的二叉查找樹具有更好的平衡,是以查找起來更快。
//查找擷取指定的值
public override TValue Get(TKey key)
{
return GetValue(root, key);
}
private TValue GetValue(Node node, TKey key)
{
if (node == null) return default(TValue);
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node.Value;
else if (cmp > 0) return GetValue(node.Right, key);
else return GetValue(node.Left, key);
} 平衡化
在介紹插入之前,我們先介紹如何讓紅黑樹保持平衡,因為一般的,我們插入完成之後,需要對樹進行平衡化操作以使其滿足平衡化。
旋轉
旋轉又分為左旋和右旋。通常左旋操作用于将一個向右傾斜的紅色連結旋轉為向左連結。對比操作前後,可以看出,該操作實際上是将紅線連結的兩個節點中的一個較大的節點移動到根節點上。
左旋操作如下圖:
//左旋轉
private Node RotateLeft(Node h)
{
Node x = h.Right;
//将x的左節點複制給h右節點
h.Right = x.Left;
//将h複制給x右節點
x.Left = h;
x.Color = h.Color;
h.Color = RED;
return x;
} 左旋的動畫效果如下:
右旋是左旋的逆操作,過程如下:
代碼如下:
//右旋轉
private Node RotateRight(Node h)
{
Node x = h.Left;
h.Left = x.Right;
x.Right = h;
x.Color = h.Color;
h.Color = RED;
return x;
} 右旋的動畫效果如下:
顔色反轉
當出現一個臨時的4-node的時候,即一個節點的兩個子節點均為紅色,如下圖:
這其實是個A,E,S 4-node連接配接,操作類似于2-3樹,我們需要将E提升至父節點,操作方法很簡單,就是把E對子節點的連線設定為黑色,自己的顔色設定為紅色。
有了以上基本操作方法之後,我們現在對比之前對2-3樹的平衡操作和對紅黑樹進行平衡操作,這兩者是可以一一對應的,如下圖:
現在來讨論各種情況:
Case 1 往一個2-node節點底部插入新的節點
先熱身一下,首先我們看對于隻有一個節點的紅黑樹,插入一個新的節點的操作:
這種情況很簡單,隻需要:
- 标準的二叉查找樹周遊即可。新插入的節點标記為紅色
- 如果新插入的節點在父節點的右子節點,則需要進行左旋操作
Case 2往一個3-node節點底部插入新的節點
先熱身一下,假設我們往一個隻有兩個節點的樹中插入元素,如下圖,根據待插入元素與已有元素的大小,又可以分為如下三種情況:
- 如果待插入的節點比現有的兩個節點都大,這種情況最簡單。我們隻需要将新插入的節點連接配接到右邊子樹上即可,然後将中間的元素提升至根節點。這樣根節點的左右子樹都是紅色的節點了,我們隻需要調研FlipColor方法即可。其他情況經過反轉操作後都會和這一樣。
- 如果插入的節點比最小的元素要小,那麼将新節點添加到最左側,這樣就有兩個連接配接紅色的節點了,這是對中間節點進行右旋操作,使中間結點成為根節點。這是就轉換到了第一種情況,這時候隻需要再進行一次FlipColor操作即可。
- 如果插入的節點的值位于兩個節點之間,那麼将新節點插入到左側節點的右子節點。因為該節點的右子節點是紅色的,是以需要進行左旋操作。操作完之後就變成第二種情況了,再進行一次右旋,然後再調用FlipColor操作即可完成平衡操作。
有了以上基礎,我們現在來總結一下往一個3-node節點底部插入新的節點的操作步驟,下面是一個典型的操作過程圖:
可以看出,操作步驟如下:
- 執行标準的二叉查找樹插入操作,新插入的節點元素用紅色辨別。
- 如果需要對4-node節點進行旋轉操作
- 如果需要,調用FlipColor方法将紅色節點提升
- 如果需要,左旋操作使紅色節點左傾。
- 在有些情況下,需要遞歸調用Case1 Case2,來進行遞歸操作。如下:
代碼實作
經過上面的平衡化讨論,現在就來實作插入操作,一般地插入操作就是先執行标準的二叉查找樹插入,然後再進行平衡化。對照2-3樹,我們可以通過前面讨論的,左旋,右旋,FlipColor這三種操作來完成平衡化。
具體操作方式如下:
- 如果節點的右子節點為紅色,且左子節點位黑色,則進行左旋操作
- 如果節點的左子節點為紅色,并且左子節點的左子節點也為紅色,則進行右旋操作
- 如果節點的左右子節點均為紅色,則執行FlipColor操作,提升中間結點。
根據這一邏輯,我們就可以實作插入的Put方法了。
public override void Put(TKey key, TValue value)
{
root = Put(root, key, value);
root.Color = BLACK;
}
private Node Put(Node h, TKey key, TValue value)
{
if (h == null) return new Node(key, value, 1, RED);
int cmp = key.CompareTo(h.Key);
if (cmp < 0) h.Left = Put(h.Left, key, value);
else if (cmp > 0) h.Right = Put(h.Right, key, value);
else h.Value = value;
//平衡化操作
if (IsRed(h.Right) && !IsRed(h.Left)) h = RotateLeft(h);
if (IsRed(h.Right) && IsRed(h.Left.Left)) h = RotateRight(h);
if (IsRed(h.Left) && IsRed(h.Right)) h = FlipColor(h);
h.Number = Size(h.Left) + Size(h.Right) + 1;
return h;
}
private int Size(Node node)
{
if (node == null) return 0;
return node.Number;
} 分析
對紅黑樹的分析其實就是對2-3查找樹的分析,紅黑樹能夠保證符号表的所有操作即使在最壞的情況下都能保證對數的時間複雜度,也就是樹的高度。
在分析之前,為了更加直覺,下面是以升序,降序和随機建構一顆紅黑樹的動畫:
- 以升序插入建構紅黑樹:
- 以降序插入建構紅黑樹:
- 随機插入建構紅黑樹
從上面三張動畫效果中,可以很直覺的看出,紅黑樹在各種情況下都能維護良好的平衡性,進而能夠保證最差情況下的查找,插入效率。
下面來詳細分析下紅黑樹的效率:
1. 在最壞的情況下,紅黑樹的高度不超過2lgN
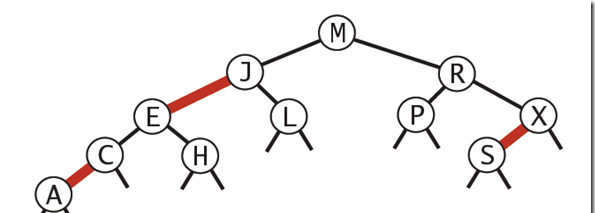
最壞的情況就是,紅黑樹中除了最左側路徑全部是由3-node節點組成,即紅黑相間的路徑長度是全黑路徑長度的2倍。
下圖是一個典型的紅黑樹,從中可以看到最長的路徑(紅黑相間的路徑)是最短路徑的2倍:
2. 紅黑樹的平均高度大約為lgN
下圖是紅黑樹在各種情況下的時間複雜度,可以看出紅黑樹是2-3查找樹的一種實作,他能保證最壞情況下仍然具有對數的時間複雜度。
下圖是紅黑樹各種操作的時間複雜度。
應用
紅黑樹這種資料結構應用十分廣泛,在多種程式設計語言中被用作符号表的實作,如:
- Java中的java.util.TreeMap,java.util.TreeSet
- C++ STL中的:map,set,multimap,multiset
- .NET中的:SortedDictionary,SortedSet 等
下面以.NET中為例,通過Reflector工具,我們可以看到SortedDictionary的Add方法如下:
public void Add(T item)
{
if (this.root == null)
{
this.root = new Node<T>(item, false);
this.count = 1;
}
else
{
Node<T> root = this.root;
Node<T> node = null;
Node<T> grandParent = null;
Node<T> greatGrandParent = null;
int num = 0;
while (root != null)
{
num = this.comparer.Compare(item, root.Item);
if (num == 0)
{
this.root.IsRed = false;
ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_AddingDuplicate);
}
if (TreeSet<T>.Is4Node(root))
{
TreeSet<T>.Split4Node(root);
if (TreeSet<T>.IsRed(node))
{
this.InsertionBalance(root, ref node, grandParent, greatGrandParent);
}
}
greatGrandParent = grandParent;
grandParent = node;
node = root;
root = (num < 0) ? root.Left : root.Right;
}
Node<T> current = new Node<T>(item);
if (num > 0)
{
node.Right = current;
}
else
{
node.Left = current;
}
if (node.IsRed)
{
this.InsertionBalance(current, ref node, grandParent, greatGrandParent);
}
this.root.IsRed = false;
this.count++;
this.version++;
}
} 可以看到,内部實作也是一個紅黑樹,其操作方法和本文将的大同小異,感興趣的話,您可以使用Reflector工具跟進去檢視源代碼。
總結
前文講解了自平衡查找樹中的2-3查找樹,這種資料結構在插入之後能夠進行自平衡操作,進而保證了樹的高度在一定的範圍内進而能夠保證最壞情況下的時間複雜度。但是2-3查找樹實作起來比較困難,紅黑樹是2-3樹的一種簡單高效的實作,他巧妙地使用顔色标記來替代2-3樹中比較難處理的3-node節點問題。紅黑樹是一種比較高效的平衡查找樹,應用非常廣泛,很多程式設計語言的内部實作都或多或少的采用了紅黑樹。