[qq群:
189191838,對算法和c++感興趣可以進來]
最近天下有一種頗不太平的感覺,各地的亂刀砍人,到處是貪官服法。京東準備上市了,阿裡最近也送出申請了,獵豹也逆襲了,據說獵豹移動在國際市場上表現甚是搶眼。隻有屌絲還在寫着代碼。花開花又謝,花謝花又開,為什麼這麼多人沒有安全感呢?是轉型社會給大家帶來了浮躁,還是什麼?不得而知!
另外,就上一篇文章的問題,還請大家各抒己見!
ok,下面進入今天的主題。紅黑樹。
我們時候用到了紅黑樹?
c++stl中map,set的底層實作全是用的紅黑樹,java,c#等語言同樣如此。
為什麼需要紅黑樹?
map,set底層都提供了排序功能,且查找速度快。紅黑樹實際上是avl的一種變形,但是其比avl(平衡二叉搜尋樹)具有更高的插入效率,當然查找效率會平衡二叉樹稍微低一點點,畢竟平衡二叉樹太完美了。但是這種查找效率的損失是非常值得的。它的操作有着良好的最壞情況運作時間,并且在實踐中是高效的:
它可以在o(log n)時間内做查找,插入和删除,這裡的n是樹中元素的數目。
何為紅黑樹?
這裡二叉平衡樹的概念我就不提了。紅黑樹是每個節點都帶有顔色屬性的二叉查找樹,顔色或紅色或黑色。
性質1
節點是紅色或黑色。
性質2
根節點是黑色。
性質3
每個葉節點(nil節點,空節點)是黑色的。
性質4
每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
性質5
從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
這些限制的好處是:保持了樹的相對平衡,同時又比avl的插入删除操作的複雜性要低許多。
操作:
我們知道平衡二叉樹要保持他的平衡性,旋轉是一項必不可少的工作。同樣,紅黑樹是一顆準平衡二叉樹,旋轉也是一項重要工作。旋轉有向左旋轉,向右旋轉,左右旋轉,右左旋轉。其實左右和右左旋轉就是左、右旋轉的二次使用,我們這裡隻談論向左旋轉、向右旋轉。
樹的旋轉:
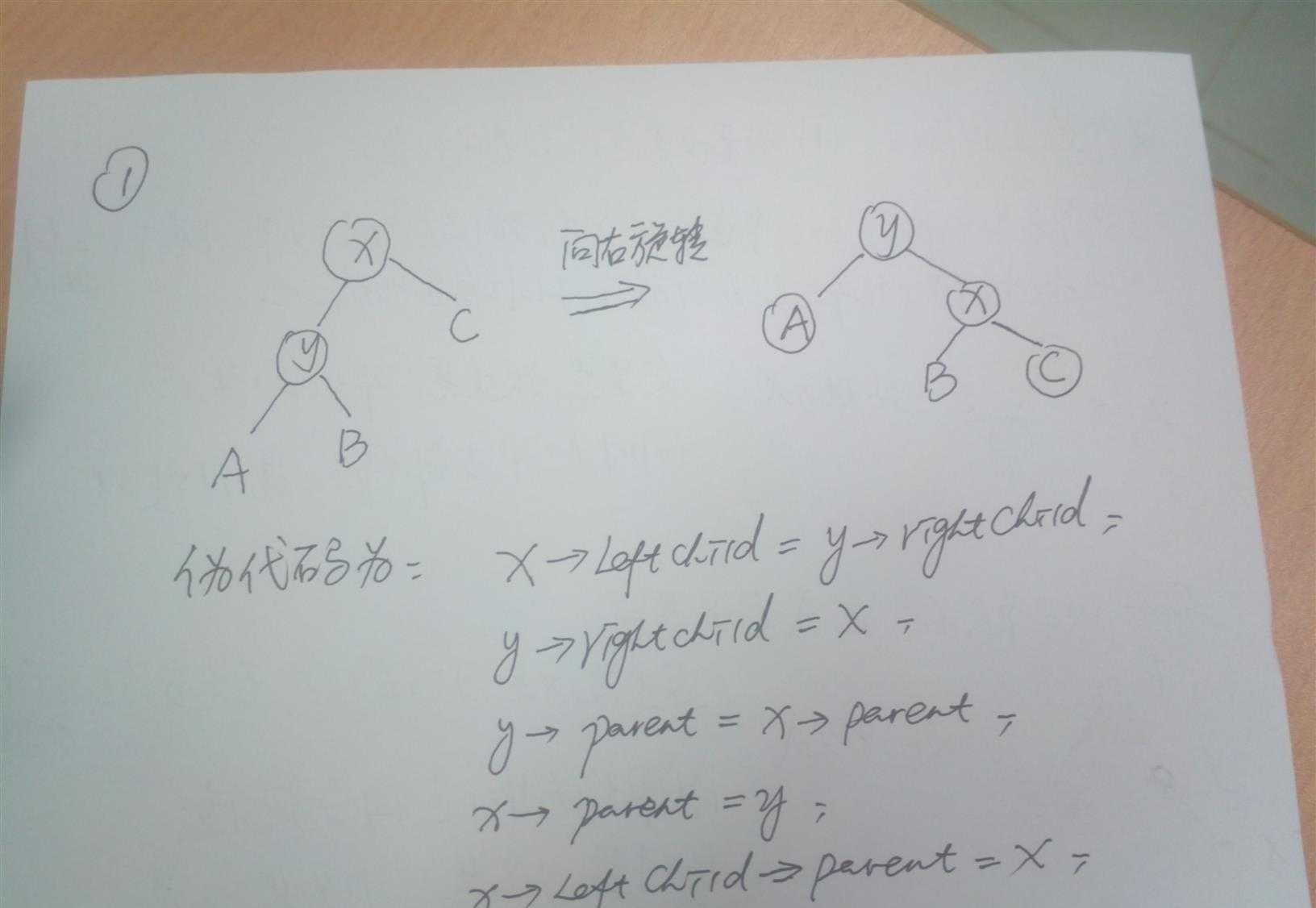
左右旋轉的就是上圖所示了,代碼如下:
紅黑樹的插入:
一直搜查到葉子節點x,x的父節點會出現以下幾種情況:
1、父節點是空,或者父節點的顔色是黑色。直接插入。
2、父節點是紅色:
1)父節點是爺爺結點的左結點
a,叔叔結點存在,且是紅色
b,叔叔結點不存在,或者是黑色
2)父節點是爺爺結點的右孩子
c,叔叔結點存在且也為紅色
d,叔叔結點不存在,或者為黑色。
第二種情況:
紅黑樹的插入操作就是上圖所示:代碼如下,
紅黑樹的删除操作類似于b-樹的删除,需要注意保持它的紅黑平衡性。紅黑的搜尋那就和b-樹的查找一模一樣了,其實任何排序樹的操作都是一樣的。比如下面将要講到的b+樹。
b樹系列還有一篇是b+樹,敬請期待。
參考文獻:stl源碼剖析、百度。
版權所有,歡迎轉載,但是轉載請注明出處: