本节书摘来自华章计算机《数学建模:基于r》一书中的第1章,第1.3节,作者:薛 毅 更多章节内容可以访问云栖社区“华章计算机”公众号查看。
1.3.1 二项分布的检验
对于单个总体,如果作n次试验,且成功的概率为p,则试验成功的次数x服从二项分布,即x~b(n,p).如果n次试验中有x次成功了,可用p=xn作为p的估计.
1.二项分布的近似检验
当np≥5且nq≥5(q=1-p)时,可用正态分布近似二项分布,即p~n(p,p q/n)(1.44)近似成立.所以p-pp q/n~n(0,1)(1.45)近似成立.因此,可以用标准正态分布作比值p的检验
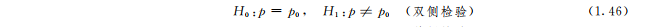
对于两个总体,如果试验次数分别为n1和n2,成功的次数分别为x1和x2,可用pi=xini作为pi(i=1,2)的估计.当nipi≥5且niqi≥5(qi=1-pi,i=1,2)时,可用正态分布近似二项分布,即p1~n(p1,p1q1/n1), p2~n(p2,p2q2/n2)(1.49)近似成立.所以当p1=p2=p(q=1-p)时,p1-p2pq1n1+1n2~n(0,1)(1.50)近似成立.因此,也可以用标准正态分布作比值差p1-p2的检验
在r中,用prop.test()函数来完成二项分布的近似检验,其使用格式为 prop.test(x, n, p = null,
alternative = c("two.sided", "less", "greater"),
conf.level = 0.95, correct = true)参数x为整数向量,表示试验成功的次数,或者为一个2列的矩阵,第1列表示成功的次数,第2列表示失败的次数.
n为整数向量,表示试验的次数,当x为矩阵时,该值无效.
p为向量,表示试验成功的概率,必须与x有相同的维数,且值在0至1之间,默认值为null.
alternative为备择假设选项,取"two.sided"(默认值)表示双侧检验;取"less"表示备择假设为“<”的单侧检验,取"greater"表示备择假设为“>”的单侧检验.
conf.level为0~1之间的数值(默认值为0.95),表示置信水平,它将用于计算比率p或比率差p1-p2的置信区间.
correct为逻辑变量,表示是否对统计量作连续修正,默认值为true.
当z~n(0,1)时,有z2~χ2(1).所以,prop.test()函数没有使用正态分布作检验,而是采用χ2分布作检验,这样做的优点是,很容易将两个总体的假设检验方法推广到m(≥3)个总体的检验中.
例1.12 某医院研究乳腺癌家族史对于乳腺癌发病率的影响.假设调查了10000名50~54岁的妇女,她们的母亲曾患有乳腺癌.发现她们在某个生存期的某个时刻有400例乳腺癌,而全国在该年龄段的妇女乳腺癌的患病率为2%,这组数据能否说明乳腺癌的患病率与家族遗传有关?
解 p0=0.02,即检验h0:p=0.02, h1:p≠0.02由于是大样本,所以可以用近似检验,即可以用prop.test()函数.> prop.test(400, 10000, p = 0.02)
0.04在输出中,有χ2统计量(x-squared)、自由度(df)、p值(p-value)和比率p的置信区间,以及比率p的估计值.
由于p值(=2.2×10-16)0.05,拒绝原假设,即乳腺癌的患病率不等于2%.置信区间[0.0363,0.0441]>0.02,说明p>0.02,即乳腺癌的患病率与家族遗传有关,而且是正相关的.
也可以作单侧检验h0:p≤0.02,h1:p>0.02,其结论是拒绝原假设(请尝试),即有乳腺癌家族史的人群会增加乳腺癌的患病率.
例1.13 为节约能源,某地区政府鼓励人们拼车出行,采取的措施是在指定的某些高速路段,载有两人以上的车辆减收道路通行费.为评价该项措施的效果,随机选取了未减收路费路段的车辆2000辆和减收路费路段的车辆1500辆,发现分别有652辆和576辆是两人以上的.这些数据能否说明这项措施实施后会提高合乘汽车的比率?
0.326 0.384p值(=0.0004278)0.05,拒绝原假设,即这两组数据的比例不相同.置信区间[-0.0906,-0.0254]<0说明p1也可以作单侧检验h0:p1≥p2,h1:p1例1.14 视频工程师使用时间压缩技术来缩短播放广告节目所需要的时间,但对较短的广告是否有效?为回答这个问题,将200名大学生随机地分成三组:第1组(57名学生)观看一个包含30s广告的电视节目录像带;第2组(74名学生)观看同样的录像带,但是是24s时间压缩版的广告;第3组(69名学生)观看20s时间压缩版的广告.观看录像带两天之后,询问这三组学生广告中品牌的名称.表1.4给出每组学生回答情况的人数.试分析三种类型广告的播放效果是否有显著差异?
解 如果三种类型的广告无显著差异,那么能回忆起品牌名称的比例应该是相同的,所以检验h0:p1=p2=p3, h1:p1,p2,p3不全相同程序(程序名:exam01<code>`</code>javascript
14.r)为x <- matrix(c(15, 32, 10, 42, 42, 59), nrow=2, byrow=t)
colnames(x) <- c("30s", "24s", "20s")
rownames(x) <- c("yes", "no")
x.yes <- x["yes", ]; x.total <- margin.table(x, 2)
0.2631579 0.4324324 0.1449275p值(= 0.0006521)0.05,拒绝原假设,说明三种类型的广告播放效果是有差异的.但从得到的比率来看,采用压缩版本1(24s)的效果最好.
2.二项分布的精确检验
对于小样本数据不能用正态分布作近似检验,而需要直接用二项分布作精确检验.
在r中,用binom.test()函数完成二项分布的精确检验,其使用格式为binom.test(x, n, p = 0.5,
alternative = c("two.sided", "less", "greater"),
conf.level = 0.95)参数x为正整数,表示试验成功的次数,或者为二维向量,第1个分量表示成功的次数,第2个分量表示失败的次数.
n为正整数,表示试验次数,当x为向量时,该值无效.
p为假设中试验成功的概率,即p0,默认值为0.5.
alternative为备择假设选项,取"two.sided"(默认值)表示双侧检验,取"less"表示备择假设为“<”的单侧检验,取"greater"表示备择假设为“>”的单侧检验.
conf.level为0~1之间的数值(默认值为0.95),表示置信水平,它将用于计算比率p的置信区间.
例1.15 设某工厂生产的一批产品的次品率p是未知的.按规定,若p≤0.01,则这批产品为可接受的;否则为不可接受的.假定从这批数据很大的产品中随机地抽取100件样品,发现其中有3件次品,那么是否接受这批产品?
解 考虑最坏情况,p0=0.01,所以检验h0:p=0.01, h1:p≠0.01此时的数据不满足np≥5的条件,所以使用精确检验.> binom.test(3, 100, p=0.01)
0.03在输出中,有p值(p-value)、比率p的置信区间,以及p的估计值.
p值(=0.07937)>0.05,无法拒绝原假设,不能认为这批产品不合格.置信区间包含0.01,也说明同样的结论.
1.3.2 符号检验
所谓符号检验就是利用样本的正负号的个数来做的检验.事实上,符号检验本质上就是二项分布检验,因为样本取正或负就相当于试验成功或失败,而且成功或失败的概率为1/2.
从前面的介绍可知,大家可根据样本数目,使用正态近似计算(prop.test函数),或者使用二项分布精确计算(binom.test函数).
例1.16 某饮料店为了解顾客对饮料的爱好情况,进一步改进工作,对顾客喜欢咖啡还是喜欢奶茶,或者两者同样爱好进行了调查.该店在某日随机地抽取了13名顾客进行了调查,顾客喜欢咖啡超过奶茶用正号表示,喜欢奶茶超过咖啡用负号表示,两者同样爱好用0表示.现将调查的结果列在表1.5中.试分析顾客是喜欢咖啡还是喜欢奶茶.
解 根据题意可检验如下假设:h0:顾客喜欢咖啡等于喜欢奶茶; h1:顾客喜欢咖啡超过喜欢奶茶以上资料中有1人(即6号顾客)表示对咖啡和奶茶有同样爱好,用0表示,因而在样本容量中不加计算,所以实际上n=12.由于n的值较小,所以选择精确二项分布检验,显著性水平取α=0.10.> binom.test(3, 12, al<code>`</code>javascript
="l", conf.level = 0.90)
exact binomial test
data: 3 and 12
number of successes =3, number of trials =12, p-value =0.073
alternative hypothesis:true probability of success is less than 0.5
90 percent confidence interval:
0.0000000 0.4752663
sample estimates:
probability of success
0.3484848p值(=0.01935)<0.05,拒绝原假设.并由置信区间[0.238,0.477]<0.5,说明生活花费指数超过北京的城市数小于12,也就是说,北京是在中位数之上.
1.3.3 符号秩检验与秩和检验
由于符号检验只考虑样本的正负号,不考虑数值的大小,因此会损失一定的信息.秩检验在某种程度上可以克服符号检验的不足,所谓秩就是样本的排序.
设x1,x2,…,xn为一组样本(不必取自同一总体),将x1,x2,…,xn从小到大排成一列,xi(i=1,2,…,n)在上述排列中的位置号记为ri,称r1,r2,…,rn为样本x1,x2,…,xn产生的秩统计量.
1.单个总体的wilcoxon符号秩检验
wilcoxon符号秩检验是作单个总体x的中位数检验,即h0:m=m0, h1:m≠m0 (双侧检验)(1.54)
h0:m≥m0, h1:mh0:m≤m0, h1:m>m0 (单侧检验)(1.56)设x1,x2,…,xn是来自总体x的样本,这里假定x的分布是连续的,且关于中位数m0是对称的.这样,将xi-m0得到的差额按递增次序排列,并根据差额的次序给出相应的秩次ri.定义xi-m0>0为正秩次,xi-m0<0为负秩次.然后按照正秩次之和进行检验,这就是秩次和检验.这种方法首先由wilcoxon提出的,所以称为wilcoxon符号秩检验.
如果原观察值的数目为n′,减去xi=m0的样本后,其样本数为n.用r(+)i表示正秩次,w表示正秩次的和,则wilcoxon统计量为w=∑ni=1r(+)i(1.57)因为n个整数1,2,…,n的总和用n(n+1)/2计算,而正秩次总和可以在区间(0,n(n+1)/2)内变动,如果观察值来自中位数为m0的某个总体的假设为真,那么wilcoxon检验统计量的取值将是秩次和的平均数,即μw=n(n+1)/4的左右变动.如果该假设不成立,则w的取值将向秩次和的两头数值靠近.这样,在一定的显著性水平下,便可进行秩次和检验.
2.两个总体的wilcoxon秩和检验
wilcoxon秩和检验是作两个总体x和y中位数差的检验h0:m1-m2=0, h1:m1-m2≠0 (双侧检验)(1.58)
h0:m1-m2≥0, h1:m1-m2<0 (单侧检验)(1.59)
h0:m1-m2≤0, h1:m1-m2>0 (单侧检验)(1.60)假定x1,x2,…,xn1是来自总体x的样本,y1,y2,…,yn2是来自总体y的样本.将样本的观察值排在一起,x1,x2,…,xn1,y1,y2,…,yn2,仍设r1,r2,…,rn1为由x1,x2,…,xn1产生的秩统计量,r1,r2,…,rn2为由y1,y2,…,yn2产生的秩统计量,则wilcoxon-mann-whitney统计量定义为u=n1n2+n2(n2+1)2-∑n2i=1ri(1.61)与单一总体的wilcoxon符号检验一样,可以通过统计量u进行检验,该检验称为wilcoxon秩和检验.
wilcox.test函数
在r中,wilcox.test()函数完成wilcoxon符号秩检验与秩和检验,其使用格式为<code>`</code>javascript
wilcox.test(x, y = null,
mu = 0, paired = false, exact = null, correct = true,