本节书摘来自异步社区《编程珠玑(续)(修订版)》一书中的第2章,第2.3节拓扑排序,作者【美】jon bentley,更多章节内容可以访问云栖社区“异步社区”公众号查看。
2.3 拓扑排序
拓扑排序算法的输入是一个有向无环图,例如:
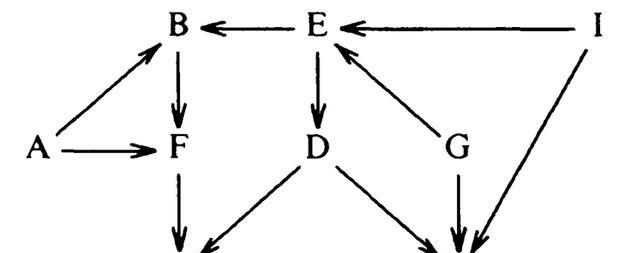
如果图中包含从a到b的边,那么a就是b的祖先而b是a的后代。算法必须对图中结点排序以使得所有祖先出现在它们的后代之前,下图是许多可能排序中的一种。
算法还必须能够处理输入图中包含回路因此无法完成排序的可能情况。
这样的算法可以应用于绘制物体的三维场景。如果物体b在视图中处于物体a的前面,那么a就在b之前,因为a必须在b之前完成绘制。下图左边由4个矩形构成的场景能够导出右边的偏序。
图2-5中有两种对顶点的有效排序,即a b c d和a c b d。每种排序都恰当地给出了物体的覆盖图。拓扑排序的其他应用包括对技术文档进行布局(术语在使用之前必须先定义)以及处理层次化vlsi设计(算法在处理一个部件之前必须先处理其组成部分)。继续阅读之前,请花一分钟思考你将如何编写对有向图进行拓扑排序的程序。
我们将研究一个拓扑排序算法,该算法引自knuth的《计算机程序设计艺术,卷1:基本算法》④一书的2.2.3节。该算法的循环步骤如下:选出一个没有祖先的结点t,将t写到输出文件中,然后从图中删除从t出发的所有边。下图显示了这个算法如何应用在之前的四结点场景图上。算法的各阶段从左向右进行,每一阶段选出的结点t都画了圈。
排序结果是a b c d。
这个算法的一种低效的实现在每一步都要扫描整个图以找到没有祖先的结点。现在来研究一个更简单也更高效的算法。对每个结点,新算法都存储它的祖先数量以及后代结点集合。比如,上面所画的四结点图表示如下:
算法的循环步骤每次选出一个祖先结点数为零的结点,把它写到输出文件中,其所有后代结点的祖先数量全部减少1。然而,算法必须仔细记住不同顶点其祖先计数变为零的先后顺序,这里使用了一个结点队列。(如果在所有结点的祖先计数变为零之前队列为空,那么程序报告图中存在回路。)
下面的伪代码假设输入给程序的图是由一系列(祖先,后代)对表示的,每行一对。
算法的运行时间与图中的边数成比例,只比最理想的情况多出一个常数因子。(每条边处理两次:一次是读,一次是从队列中将其删除。)
awk程序使用一个索引范围是1..n的数组来实现队列。整型变量qlo是队列首元素的索引,qhi是尾元素的索引。后代集合由两个数组实现。如果a有后代b、c、d,那么下面的关系成立:
这个awk程序的输入是一个祖先-后代对文件,其输出是排序好的结点列表或关于这样的列表不存在的警告。
程序第二行保证所有结点都作为predct的索引出现,即便没有祖先的结点也一样。
本程序的关联数组表示了几种不同的抽象数据类型:一个结点名字的符号表、一个记录数组、一个二维的后代集合序列以及一个结点队列。本程序小巧、便于理解,但在较大的程序中无法清楚分辨不同的抽象数据类型就会降低程序可读性。