本节书摘来自异步社区《haskell并行与并发编程》一书中的第2章,第2.1节惰性求值和弱首范式,作者【英】simon marlow,更多章节内容可以访问云栖社区“异步社区”公众号查看
2.1 惰性求值和弱首范式
haskell并行与并发编程
haskell是一门惰性语言,即表达式是在其值需要使用时才被求值2。一般来说,不必担心该过程如何发生,只要表达式在需要时求值,不需要时不被求值即可。但是,当在代码中使用了并行编程后,就需要告诉编译器一些程序运行的信息,即某些代码应该并行执行。由于对惰性求值的工作方式有一个直觉的认识将有助于有效地进行并行编程,因此本节将以ghci作为试验工具,探讨惰性求值的一些基本概念。
下面从非常简单内容的开始:
<code>prelude> let x = 1 + 2 :: int</code>
这会将变量x绑定(bind)到表达式1 + 2(为了避免任何由重载带来的复杂性,特指定为int类型)。此时,仅考虑haskell语言本身,1 + 2是和3相等的,因此这里也可以写成let x = 3 :: int,而且通过普通的haskell代码无法将两种写法区分开。但出于并行编程的目的,这里确实在意1 + 2和3的区别,因为1 + 2是一个还未开始的计算,其值也许可以通过其他方法并行地计算出来。当然,在实际中不会对像1 + 2这样简单情况使用并行计算,然而,其作为未求值计算的本质是仍然是重要的。
此刻,称x为未求值的(unevaluated)。一般来说,在haskell中是无法得知x是未求值的,但幸运的是,ghci的调试器提供了一些命令,这些命令可以查看haskell表达式的结构,但又不影响表达式本身。因此,可以通过使用这些命令来说明发生的情况。:sprint这条命令可以打印出表达式的值,但又不会引发表达式求值。
`prelude> :sprint x
x = _`
特殊符号_表示“未求值的”,对于这种情况,读者也许听过另一个词“thunk”,即内存中表示1 + 2这个未求值计算的对象。此例中的thunk如图2-1所示。
图2-1 表示1 + 2的thunk
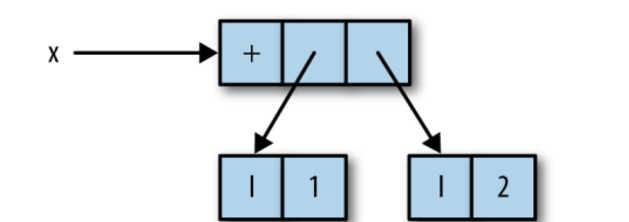
在图中,x是一个指向内存对象的指针,该内存对象表示函数+应用于整数1和2。
该thunk表示x将在其值需要时被求值。在ghci中,触发求值最容易的方法是将其打印出来,也就是说,在提示符后输入x即可:
`prelude> x
3`
现在若通过:sprint查看x的值,可以发现其已被求值:
x = 3`
从内存中的对象方面考虑,即表示1 + 2的thunk实际上被(装箱的)整数3覆盖了3。因此,以后任何对x值的查询都会立即返回结果,这就是惰性求值的工作原理。
前面的例子比较简单,再试一个稍为复杂的的示例:
`prelude> let x = 1 + 2 :: int
prelude> let y = x + 1
prelude> :sprint x
x = _
prelude> :sprint y
y = _`
这里再次将变量x绑定到1 + 2,此外,还将变量y绑定到x + 1,然后,正如所预期的,:sprint命令显示两者均未被求值。在内存中,会有图2-2所示的结构。
图2-2 一个引用了另外的thunk的thunk
不幸的是,该结构无法被直接查看,读者只有相信这里所画的图是正确的。
现在,为了计算y的值,需要x的值,即y依赖于x。因此,对y的求值同时会导致对x的求值。这次使用不同方法来强制求值,即通过haskell内建的seq函数。
`prelude> seq y ()
()`
函数seq先对其第一个参数求值,这里是y,然后返回第二个参数,此例中,即()。再查看此时x和y的值:
x = 3
y = 4`
正如所预期的,两者均已被求值。因此,到目前为止一般性的原则如下。
• 定义一个表达值会建立一个thunk来表示该表达式。
• 在需要其值前,thunk保持未求值状态。一旦被求值,则会被求出的值所替代。
再看一下增加一个数据结构会发生什么情况:
prelude> let z = (x,x)
变量z绑定到了序对(x,x),命令:sprint显示出一些有意思的内容:
prelude> :sprint z
z = (_,_)`
这里隐含的结构如图2-3所示。
变量z本身引用了序对(x,x),但序对的两项均指向了未求值的,代表x的thunk。这说明数据结构可以使用未求值的表达式来构建。
图2-3 两项引用同一thunk的序对
下面再次将z变为thunk:
`prelude> import data.tuple
prelude data.tuple> let z = swap (x,x+1)`
函数swap的定义为:swap(a,b)=(b,a)。这次z和前面的一样,是未求值的:
`prelude data.tuple> :sprint z
z = _`
这样的话,当使用seq来对z求值时,就能看清楚具体发生的情况:
`prelude data.tuple> seq z ()
()
prelude data.tuple> :sprint z
函数seq执行后,导致作为参数的z被求值,成为一个序对,但序对的两项仍然处于未求值状态。函数seq仅对其第一个参数的第一层构造求值,不再对剩下的结构继续求值。对此有一个专门的称呼:称函数seq对第一个参数求值,使之成为弱首范式(weak head normal form)。该术语的使用是出于历史原因,因此对其不必深究。该术语常被缩写为whnf4。名词范式在这里是“完全求值”5的意思,在2.4节会看到如何将表达式求值使之成为范式。
弱首范式的概念在下面两章会多次出现,因此值得去花些时间去理解这个概念,并对haskell中求值是如何发生的有所体会。对此在ghci中试验不同的表达式和:sprint命令不失为一种很好的方法。
为了完成本例,下面对x进行求值:
`prelude data.tuple> seq x ()
此时z会是何值?
z = (_,3)`
记得变量z被定义为swap(x,x+1),即(x+1,x),前面刚对x求值了,所以z的第二个成员是已被求值的,值为3。
最后,来看一个关于列表和几个常见列表函数的例子。对于函数map的定义,读者或许已经知道,不过还是列在下面作为参考:
`map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (x:xs) = f x : map f xs`
函数map建立了一个惰性的数据结构。若重写map的定义而让thunk明确,可能会更清楚一些:
map f (x:xs) = let
这和前面的map的定义是一样的,但可以看到map返回的列表的头和尾各自都是thunk:f x和map f xs。也就是说,map建立了图2-4所示的结构。
图2-4 通过map建立的thunk
下面使用map定义一个简单的列表结构:
<code>prelude> let xs = map (+1) [1..10] :: [int]</code>
此时xs未被求值:
`prelude> :sprint xs
xs = _`
接着对该列表求值,使之成为弱首范式:
`prelude> seq xs ()
prelude> :sprint xs
xs = _ : _`
目前为止,只知道xs是一个至少包含一个元素的列表。接着,对该列表应用length函数:
`prelude> length xs
10`
函数length的定义如下:
`length :: [a] -> int
length [] = 0
length (_:xs) = 1 + length xs`
注意到length会忽略列表的头,而只对列表的尾xs进行递归,因而对列表应用length时,列表的结构会被展开,但元素不会被求值。这点通过:sprint可以清楚地看到:
xs = [_,_,_,_,_,_,_,_,_,_]`
ghci注意到列表已被展开,所以改用方括号显示列表,而不再使用:。
即使通过求值的方式展开了整个列表,该列表仍不是范式(而仍然是弱首范式)。通过对列表应用一个函数,该函数需要使用列表的所有元素,就可以使之完全求值。例如sum函数:
`prelude> sum xs
65
xs = [2,3,4,5,6,7,8,9,10,11]`
前面这些讨论,对于惰性求值这个精妙而复杂的主题仅触及了表面。幸运的是,多数情况下,编写haskell代码无需了解或担心求值是何时进行的。的确,haskell语言定义十分仔细,不对如何求值作明确指定;语言的实现可以自由地选择策略,只需保证结果正确。这也是程序员大多数时候所关注的。但是,当编写并行代码时,了解表达式何时被求值变得重要起来,因为只有这样才能对并行化计算进行安排。
第4章使用par monad,对数据流进行明确的描述,是另一种使用惰性求值进行并行编程的方法。该方法牺牲了部分简洁性从而避免了一些惰性求值相关的微妙的问题。由于会出现一种方法比另一种解决问题更自然或更高效的情况,因此两种方法都值得学习。
__
1weak head normal form,函数式编程中的一种范式。——译者注
2技术上说,这并不正确。haskell实际上是一门非严格(non-strict)的语言,惰性求值只是几种正确的实现策略之一。不过ghc使用的是惰性求值,因此这里忽略这个技术细节。
3严格地说,是被一个到该值的间接引用所覆盖,不过这些细节在这里并不重要。感兴趣的读者可以到ghc wiki上阅读关于该实现的文档,以及许多关于该设计的论文。
4即弱首范式英文weak head normal form的首字母缩写。——译者注
5即表达式里面所有的部分、各层次均被求值,不存在未求值的部分。——译者注