编程之美: 求二叉树中节点的最大距离》的好解法

转自 ：http://aclay.blog.163.com/blog/static/208468235201272392954636/

昨天花了一个晚上为《编程之美》，在豆瓣写了一篇书评《迟来的书评和感想──给喜爱编程的朋友》。书评就不转载到这里了，取而代之，在这里介绍书里其中一条问题的另一个解法。这个解法比较简短易读及降低了空间复杂度，或者可以说觉得比较「美」吧。

问题定义

如果我们把二叉树看成一个图，父子节点之间的连线看成是双向的，我们姑且定义"距离"为两节点之间边的个数。写一个程序求一棵二叉树中相距最远的两个节点之间的距离。

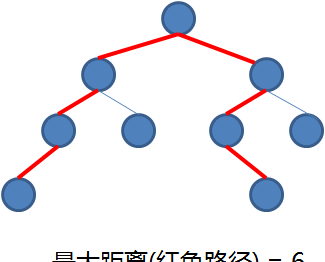
书上的解法

书中对这个问题的分析是很清楚的，我尝试用自己的方式简短覆述。

计算一个二叉树的最大距离有两个情况:

• 情况A: 路径经过左子树的最深节点，通过根节点，再到右子树的最深节点。
• 情况B: 路径不穿过根节点，而是左子树或右子树的最大距离路径，取其大者。

只需要计算这两个情况的路径距离，并取其大者，就是该二叉树的最大距离。

我也想不到更好的分析方法。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;

struct node { //
    node* left;
    node* right;
};
struct Result { // 记录的最大深度 和 最大距离
    int MaxDis;
    int MaxDep;
};

Result get_dis(node* root) {
    if(!root) {
        Result empty = {0, -1}; //trick: nMaxDepth is -1 and then caller will plus 1 to balance it as zero
        return empty;
    }
    Result lhs = get_dis(root->left);
    Result rhs = get_dis(root->right);
    Result res;
    res.MaxDep = max(lhs.MaxDep, rhs.MaxDep) + 1;
    res.MaxDis = max(max(lhs.MaxDis, rhs.MaxDis), lhs.MaxDep + rhs.MaxDep + 2);
    return res;
}
void link(node* arr, int par, int left, int right) {
    if(left != -1) {
        arr[par].left = &arr[left];
    }
    if(right != -1) {
        arr[par].right = &arr[left];
    }
}
int main() {
    node arr[105] = {0};
    link(arr, 0, 1, 2);
    link(arr, 1, 3, 4);
    link(arr, 2, 5, 6);
    link(arr, 3, 7, -1);
    link(arr, 5, -1, 8);
    cout << get_dis(&arr[0]).MaxDis << endl;
    return 0;
}


  

        

 评论这张

转发至微博