前面两期我们介绍了plot函数的绘图作用,这一期我们继续学习三维曲面的Matlab绘制函数。
以马鞍面为例,其方程为:
z = x²/a²-y²/b²
在命令行窗口输入:
>> x=-2:0.1:2;
>> y=-2:0.1:2;
意为从-2到2每隔0.1记录一个数,生成一个数组,0.1是步长。记得后面加“;”,不即时输出结果。
>> [X,Y]=meshgrid(x,y);
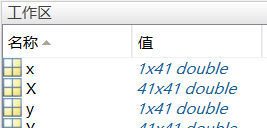
meshgrid的作用是生成一个网格矩阵,从工作区的变量属性可以看出,X和Y都是41×41的矩阵。
为什么要生成矩阵呢?因为对于曲面方程z = x²/a²-y²/b²而言,每一个x都会对应一列y值,同时每一个y也会对应一列x值。那么,z坐标方向的值的数量应该是x和y两个数组维数的乘积,所以是41×41。
>> Z=X.^2/3-Y.^2/3;
注意这里不是X^2,而是X.^2,因为X是一个矩阵,所以有一点和没一点是有区别的。
X^2是矩阵之间的乘法(X必须是方阵),X.^2则是矩阵中每个元素做平方运算。
接下来就可以用surf函数绘制曲面了,输入:
>> surf(X,Y,Z);
>> axis equal;
>> view(-30,20);
得到结果如下
曲面上的网格映射到XY平面就是[X,Y],也就是meshgrid函数生成的矩阵;view的作用则是调整图片的观察视角。(如果x和y数组的步长越小,生成的网格就会越密。曲面看上去就会一片黑,放大后才能看清网格)
继续输入:
>> shading interp
(除去网格)
>> colorbar
(添加颜色标尺)
曲面的配色可以用colormap调节,最常见的是colormap('jet'),输入后结果如下:
如果不熟悉MATLAB中的函数用法,可以用help函数(一个很有用的函数)查询,如:
可以看到colormap内置的配色方式有很多种:
比如colormap('copper'),结果如下:
今天就讲这么多,在后面的学习过程中,我们还会经常用到矩阵的思维。不要害怕矩阵这两个字,数学不好也不用担心。小编负责搞定数学,你们只需要熟悉语言就行了。
像这一期提到的函数,meshgrid、surf、colormap等,关看字面意思就能猜个八九不离十,需要记的只是函数后面用到哪些参数。
现在,Matlab的面纱才刚揭开一角而已,更多有意思的功能还在等我们去发掘。