机器学习——逻辑斯特回归（包含梯度下降推导）

文章目录

• 1. 前言
• 2. Logistic Regression模型
• • 2.1 公式
  • 2.2 Sigmoid函数
  • 2.3 Logistic Regression模型的损失函数
  • 2.3 Logistic Regression模型的梯度下降
  • • 2.3.1 sigmoid函数的求导形式
    • 2.3.2 LR函数的求导

1. 前言

在之前已经简单阐述了“线性回归”模型，具体的介绍地址为：https://blog.csdn.net/qq_30232405/article/details/104153928

这种简单的线性回归在拟合复杂模型的时候，会出现拟合能力不足的情况。

例如下图已经存在的数据：

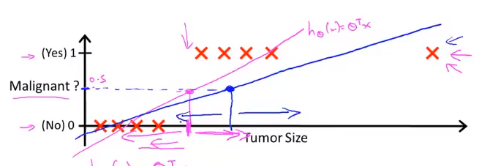
• 横坐标表示：tumor size（肿瘤大小），用 x x x表示。

• 横坐标：malignant（恶行肿瘤），可以用如下公式表示：

  h θ ( x ) = θ T x h_\theta(x) = \theta^{\mathrm{T}}x hθ​(x)=θTx

图中有两条拟合线：

• 粉红色直线：当图中没有最右异常点的时候，可以用线性回归进行拟合
• 蓝色直线：当图中有最右异常点时，用直线拟合的。

如果一开始设置了 h θ ( x ) h_\theta(x) hθ​(x)大于0.5时，默认类别为1（恶性肿瘤），少于0.5时类别为0（良性肿瘤），则粉红色的直线对应的曲线恰好可以有效区分两种类别。但是蓝色直线对应的 x x x坐标则向左偏移，这时候会把肿瘤错误预测为0。

为了能够得到更有效的模型，则需要logistic regression（LR）模型来解决这个问题。

2. Logistic Regression模型

2.1 公式

首先展示LR模型的公式：

h θ ( x ) = g ( θ T x ) g ( θ T x ) = 1 1 + e − θ T x h_\theta(x) = g(\theta^{\mathrm{T}}x) \\ g(\theta^{\mathrm{T}}x)= \frac{1}{1+e^{-\theta^{\mathrm{T}}x}} hθ​(x)=g(θTx)g(θTx)=1+e−θTx1​

可以看到，LR模型在普通的线性回归中增加了函数 g g g，如果把 z = θ T x z=\theta^{\mathrm{T}}x z=θTx，可以把 g g g公式化简为：

g ( z ) = 1 1 + e − z g(z)= \frac{1}{1+e^{-z}} g(z)=1+e−z1​

这个公式就是典型的sigmoid函数，也可以称为是logistic函数。

2.2 Sigmoid函数

现在观察一下sigmoid函数的图像形状：

• 当 z z z趋向于infinity时， g ( z ) g(z) g(z)接近于1
• 当 z z z趋向于infinitesimal时， g ( z ) g(z) g(z)接近于0

用上面“预测肿瘤是否为恶性”的例子，不难看出 h θ ( x ) h_\theta(x) hθ​(x)的输出值就代表肿瘤是否为恶性的概率。

例如：当 h θ ( x ) = 0.7 h_\theta(x)=0.7 hθ​(x)=0.7，也就是说该肿瘤有70%的概率会是恶性肿瘤。所以，如果给定 x x x和 θ \theta θ的值，预测 y y y的概率可以表示为：

h θ ( x ) = P ( y ∣ x ; θ ) h_\theta(x)=P(y|x;\theta) hθ​(x)=P(y∣x;θ)

对于两分类来说，这种函数两个性质：

• P ( y = 0 ∣ x ; θ ) + P ( y = 1 ∣ x ; θ ) = 1 P(y=0|x;\theta)+P(y=1|x;\theta)=1 P(y=0∣x;θ)+P(y=1∣x;θ)=1
• P ( y = 0 ∣ x ; θ ) = 1 − P ( y = 1 ∣ x ; θ ) P(y=0|x;\theta)=1-P(y=1|x;\theta) P(y=0∣x;θ)=1−P(y=1∣x;θ)

2.3 Logistic Regression模型的损失函数

回归一下，之前的线性回归模型的损失函数为：

J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1​i=1∑m​(hθ​(x(i))−y(i))2

也可以用另外的符号来表示：

C o s t ( h θ ( x ) , y ) = J ( θ ) Cost(h_\theta(x), y)=J(\theta) Cost(hθ​(x),y)=J(θ)

如果我们把线性回归的损失函数 J ( θ ) J(\theta) J(θ)以图像的形式画出来：

可以看到这个函数是凸函数，可以求出全局最优点。

而如果把 h θ ( x ) h_\theta(x) hθ​(x)换成LR模型的函数，同时画出其 J ( θ ) J(\theta) J(θ)的图像

这时候函数是非凸函数，存在很多的局部最优点。所以需要像一个新的损失函数，它应该具有两个基本的性质：

• 能够代表预测函数和正确类别之间的距离。
• 最好函数是一个凸函数，具有全局最优点。

因此研究者找到了一个比较适合的损失函数：

C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) )    i f   y = 1 − l o g ( 1 − h θ ( x ) )    i f   y = 0 Cost(h_\theta(x), y)=\left\{ \begin{aligned} -log(h_\theta(x)) ~~ if~y=1 \\ -log(1-h_\theta(x)) ~~ if~y=0\\ \end{aligned} \right. Cost(hθ​(x),y)={−log(hθ​(x))  if y=1−log(1−hθ​(x))  if y=0​

为什么要引入这样的损失函数呢，接下来可以用对应的图像进行解释。

• 当 y = 1 y=1 y=1时，其损失函数图像为：

  

  由于真实标签为1，当 h θ ( x ) h_\theta(x) hθ​(x)接近于1时，说明此时函数的预测与真实标签是一致的，那么损失函数的值就接近于0。如果要进行参数更新，这时候由于损失函数接近0，参数几乎不用更新。当 h θ ( x ) h_\theta(x) hθ​(x)接近于0时，说明此时函数的预测与真实标签是不一致的，这会导致损失函数的值增大，需要更快的更新参数。
• 当 y = 0 y=0 y=0时，其损失函数图像为：

  

  其性质说明和上面的图像一致，这就不详细说明了。

2.3 Logistic Regression模型的梯度下降

首先对上面的LR公式进行合并：

J ( θ ) = C o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) J(\theta) =Cost(h_\theta(x^{(i)}), y^{(i)})= -\frac{1}{m} \sum_{i=1}^{m} y^{(i)} log(h_\theta(x^{(i)})) +(1-y^{(i)} )log(1-h_\theta(x^{(i)} )) J(θ)=Cost(hθ​(x(i)),y(i))=−m1​i=1∑m​y(i)log(hθ​(x(i)))+(1−y(i))log(1−hθ​(x(i)))

• 当 y ( i ) = 1 y^{(i)}=1 y(i)=1时，则会变成:

  J ( θ ) = − 1 m ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) J(\theta)= -\frac{1}{m} \sum_{i=1}^{m} y^{(i)} log(h_\theta(x^{(i)})) J(θ)=−m1​i=1∑m​y(i)log(hθ​(x(i)))

• 当 y ( i ) = 0 y^{(i)}=0 y(i)=0时，则会变成:

  J ( θ ) = − 1 m ∑ i = 1 m ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) J(\theta)= -\frac{1}{m} \sum_{i=1}^{m} (1-y^{(i)} )log(1-h_\theta(x^{(i)} )) J(θ)=−m1​i=1∑m​(1−y(i))log(1−hθ​(x(i)))

利用梯度下降法，如果要求出最优参数 θ \theta θ，则需要最小化 J ( θ ) J(\theta) J(θ)，同时更新参数：

θ j : = θ j − α ∂ J ( θ ) ∂ θ j \theta_j:=\theta_j- \alpha \frac{\partial J(\theta)}{\partial \theta_j} θj​:=θj​−α∂θj​∂J(θ)​

要对上面这个偏导数求解，首先要知道sigmoid函数求导后的形式。

2.3.1 sigmoid函数的求导形式

∂ g ( z ) ∂ z = ∂ ∂ z 1 1 + e − z = e − z ( 1 + e − z ) 2 = 1 1 + e − z − 1 ( 1 + e − z ) 2 = g ( z ) ( 1 − g ( z ) ) \frac{\partial g(z)}{\partial z} = \frac{\partial }{\partial z} \frac{1}{1+e^{-z}} =\frac{e^{-z}}{(1+e^{-z})^2} = \frac{1}{1+e^{-z}} - \frac{1}{(1+e^{-z})^2} =g(z)(1-g(z)) ∂z∂g(z)​=∂z∂​1+e−z1​=(1+e−z)2e−z​=1+e−z1​−(1+e−z)21​=g(z)(1−g(z))

可以看到sigmoid函数的求导形式有一个很特别的地方：它的求导形式都可以用原函数表示。最后得到公式：

g ( z ) ′ = g ( z ) ( 1 − g ( z ) ) g(z)^{'}=g(z)(1-g(z)) g(z)′=g(z)(1−g(z))

如果对 g ( θ T x ) g(\theta^{\mathrm{T}}x) g(θTx)求导，其过程差不多，但是会多出一个 x j ( i ) x^{(i)}_j xj(i)​相乘：

∂ g ( θ T x ) ∂ θ j = g ( θ T x ) ( 1 − g ( θ T x ) ) x j ( i ) \frac{\partial g(\theta^{\mathrm{T}}x)}{\partial \theta_j}=g(\theta^{\mathrm{T}}x)(1-g(\theta^{\mathrm{T}}x))x^{(i)}_j ∂θj​∂g(θTx)​=g(θTx)(1−g(θTx))xj(i)​

• 要注意的是 θ \theta θ和 x x x都是一个向量形式

2.3.2 LR函数的求导

有了上述sigmoid函数的求导形式作为背景，我们可以化简 ∂ J ( θ ) ∂ θ j \frac{\partial J(\theta)}{\partial \theta_j} ∂θj​∂J(θ)​。在损失函数 J ( θ ) J(\theta) J(θ)中， θ \theta θ和 x x x都是一个向量形式，也就是：

θ = [ θ 0 , θ 1 , . . . , θ n ] x = [ x 0 , x 1 , . . . , x n ] \theta=[\theta_0,\theta_1,...,\theta_n] \\ x=[x_0,x_1,...,x_n] θ=[θ0​,θ1​,...,θn​]x=[x0​,x1​,...,xn​]

当我们仅仅针对 θ j \theta_j θj​进行求导的时候：

∂ J ( θ ) ∂ θ j = − 1 m ∑ i m y ( i ) h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ θ j − 1 − y ( i ) 1 − h θ ( x ( i ) ) ∂ h θ ( x ( i ) ) ∂ θ j = − 1 m ∑ i m y ( i ) g ( θ T x ) ∂ g ( θ T x ) ∂ θ j − 1 − y ( i ) 1 − g ( θ T x ) ∂ g ( θ T x ) ∂ θ j \frac{\partial J(\theta)}{\partial \theta_j} = -\frac{1}{m} \sum_i^{m} \frac{y^{(i)}}{h_\theta(x^{(i)})} \frac{\partial h_\theta(x^{(i)})}{\partial \theta_j} - \frac{1-y^{(i)}}{1-h_\theta(x^{(i)})} \frac{\partial h_\theta(x^{(i)})}{\partial \theta_j} \\ = -\frac{1}{m} \sum_i^{m} \frac{y^{(i)}}{g(\theta^{\mathrm{T}}x)} \frac{\partial g(\theta^{\mathrm{T}}x)}{\partial \theta_j} - \frac{1-y^{(i)}}{1-g(\theta^{\mathrm{T}}x)} \frac{\partial g(\theta^{\mathrm{T}}x)}{\partial \theta_j} ∂θj​∂J(θ)​=−m1​i∑m​hθ​(x(i))y(i)​∂θj​∂hθ​(x(i))​−1−hθ​(x(i))1−y(i)​∂θj​∂hθ​(x(i))​=−m1​i∑m​g(θTx)y(i)​∂θj​∂g(θTx)​−1−g(θTx)1−y(i)​∂θj​∂g(θTx)​

可以看到上面需要利用sigmoid函数的求导方法：

∂ J ( θ ) ∂ θ j = − 1 m ∑ i m y ( i ) g ( θ T x ) g ( θ T x ) ( 1 − g ( θ T x ) ) x j ( i ) − 1 − y ( i ) 1 − g ( θ T x ) g ( θ T x ) ( 1 − g ( θ T x ) ) x j ( i ) = − 1 m ∑ i m y ( i ) ( 1 − g ( θ T x ) ) x j ( i ) − ( 1 − y ( i ) ) g ( θ T x ) x j ( i ) = 1 m ∑ i m ( g ( θ T x ) − y ( i ) ) x j ( i ) = 1 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J(\theta)}{\partial \theta_j} = -\frac{1}{m} \sum_i^{m} \frac{y^{(i)}}{g(\theta^{\mathrm{T}}x)} g(\theta^{\mathrm{T}}x)(1-g(\theta^{\mathrm{T}}x))x^{(i)}_j - \frac{1-y^{(i)}}{1-g(\theta^{\mathrm{T}}x)} g(\theta^{\mathrm{T}}x)(1-g(\theta^{\mathrm{T}}x))x^{(i)}_j \\ =-\frac{1}{m} \sum_i^{m} y^{(i)} (1-g(\theta^{\mathrm{T}}x))x^{(i)}_j - (1-y^{(i)})g(\theta^{\mathrm{T}}x)x^{(i)}_j \\ =\frac{1}{m} \sum_i^{m}(g(\theta^{\mathrm{T}}x) - y^{(i)})x^{(i)}_j \\ =\frac{1}{m} \sum_i^{m}(h_\theta(x^{(i)}) - y^{(i)})x^{(i)}_j ∂θj​∂J(θ)​=−m1​i∑m​g(θTx)y(i)​g(θTx)(1−g(θTx))xj(i)​−1−g(θTx)1−y(i)​g(θTx)(1−g(θTx))xj(i)​=−m1​i∑m​y(i)(1−g(θTx))xj(i)​−(1−y(i))g(θTx)xj(i)​=m1​i∑m​(g(θTx)−y(i))xj(i)​=m1​i∑m​(hθ​(x(i))−y(i))xj(i)​

至此，LR的损失函数的求导形式已经结束，这里面主要用到了sigmoid函数的求导，推导起来其实是比较简单的。最后写出梯度下降的更新公式：

θ j : = θ j − α 1 m ∑ i m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j- \alpha \frac{1}{m} \sum_i^{m}(h_\theta(x^{(i)}) - y^{(i)})x^{(i)}_j θj​:=θj​−αm1​i∑m​(hθ​(x(i))−y(i))xj(i)​

对比一下线性回归的梯度下降公式：

θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x j ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \alpha \frac{1}{m} \sum^{m}_{i=1} (h_{\theta}(x^{(i)}_j) - y^{(i)}) x^{(i)}_j θj​:=θj​−αm1​i=1∑m​(hθ​(xj(i)​)−y(i))xj(i)​

发现他们两个的公式高度统一，佩服以前的研究工作者能够想出这么完美的损失函数。