天天看点
返回

Link Cut Tree入门

LCT 是 link cut tree 的简称，顾名思义~ 就是树带动态的增删边的操作.

分析

题目背景

动态树

题目描述

给定 n 个点以及每个点的权值，要你处理接下来的 m 个操作。

操作有四种，操作从 0 到 3 编号。点从 1 到 n 编号。

0 x y 代表询问从 x 到 y 的路径上的点的权值的 xor 和。保证 x 到 y 是联通的。

1 x y 代表连接 x 到 y，若 x 到 y 已经联通则无需连接。

2 x y 代表删除边 (x,y)，不保证边 (x,y) 存在。

3 x y 代表将点 x 上的权值变成 y。

输入格式

第一行两个整数，分别为 n 和 m，代表点数和操作数。

接下来 n 行，每行一个整数，整数在 [1,1e9] 内，代表每个点的权值。

然后有 m 行，每行三个整数，分别代表操作类型和操作所需的量。

输出格式

对于每一个 0 号操作，你须输出一行一个整数，表示 x 到 y 的路径上点权的 xor 和。

输入输出样例

输入 #1复制

3 3

1

2

3

1 1 2

0 1 2

0 1 1

输出 #1复制

3

1

输入 #2复制

5 14

114 514 19 19 810

1 1 2

0 1 2

2 1 2

1 1 2

1 2 3

2 1 3

1 1 3

1 4 5

1 2 5

0 3 5

0 3 4

3 5 233333

0 1 5

0 2 5

输出 #2复制

624

315

296

232709

232823

说明/提示

【数据范围】

对于 100% 的数据， 1<=n<=1e5, 1<=m<=3e5

lct是一种动态维护森林结构的算法，它可以让一个森林支持很多动态的操作——比如连边（link）、断边（cut）、换根（mkrt）、查询树链信息....

其实lct就是树剖的加强版——只不过树剖采用线段树维护树链，所以树剖能解决的一般是比较偏向静态树链问题，但是lct使用splay来维护树链信息, 所以自然的，splay是lct的前置技能~

针对本题的splay的节点的数据结构如下

struct SplayNode
{
    int val, fa, lc, rc, xr, lz; // 当前节点的权值, 父节点, 左孩子, 右孩子, 以当前节点为根的splay子树的所有节点的异或和, 以当前节点为根的splay子树的翻转次数(这是一个懒标记)
};

复制

本题其实树剖不方便搞的操作就是1+2

树剖的话，我们学过重链剖分和长链剖分，而lct操作过程中产生树剖称之为实链剖分——因为lct操作的过程中会产生一系列的实边和虚边.

重链剖分中的概念换个名字到实链剖分中，那么我们自然就有 实链、实儿子、虚儿子、实边、虚边 这些概念 ...

重链剖分使用线段树维护每根重链，类比的, lct使用splay维护每条实链.

首先我们大致来看看lct长什么样子?

下面图2就是原树的样子, 而图3就是其一种（注意，仅仅是一种）lct. 换言之, lct就是原树中的一些连通块的不交并, 连通块内部的节点使用图3中的实线（即实边）连接，但是这些实边未必是原树中的边，而这些连通块之间通过图3中的虚线（即虚边）连接在一起，这些虚边也未必是原树中的边. 那么什么才叫lct呢?

1. 原树的每个节点在且仅在一个连通凸块（即两个点在其中, 则此两点之间路径上的所有点都在其中，下面简称连通凸块为连通块）中, 即lct是原树上的一些连通块的不交并. 2. 连通块是树，而且关于在原树中的深度（下面简称深度）构成bst（二叉搜索树）,例如图3中的连通块CGJH在原树中的深度分别是2、3、5、4，而该连通块如果视作树的话，关于此深度指标恰好是构成bst的.

所以如果学过动态点分治的点分树的话，就比较好理解lct了——它其实就是原树的某种重构树. 连通块内部点之间的边就是实链剖分中的实边, 连通块之间的连边就是实链剖分中的虚边, emmm, 这种感觉很树剖~

为什么连通块要关于深度形成bst? 因为原树上的连通块一定也是树，现在如果告诉你这棵树上的点在原树中的深度形成bst的话，你会发现什么? 对的，那就是这个连通块其实在原树上是一根链！也就是前面提到的所谓的实链， 所以其实lct就是原树的实链剖分。这就非常自然的将lct和实链剖分对应到一起了.

lct中使用splay这种bst来维护上面说的连通块（实链）, 至于为什么, 后面会说, 现在暂且按住不表.

所以lct就是将原树剖分成了一棵一棵的splay, 这些splay对应树上的连通块，也就是一根一根的实链. 因为每条实链是由一棵splay维护的， 所以每个节点只能包含且仅包含在一棵splay中.

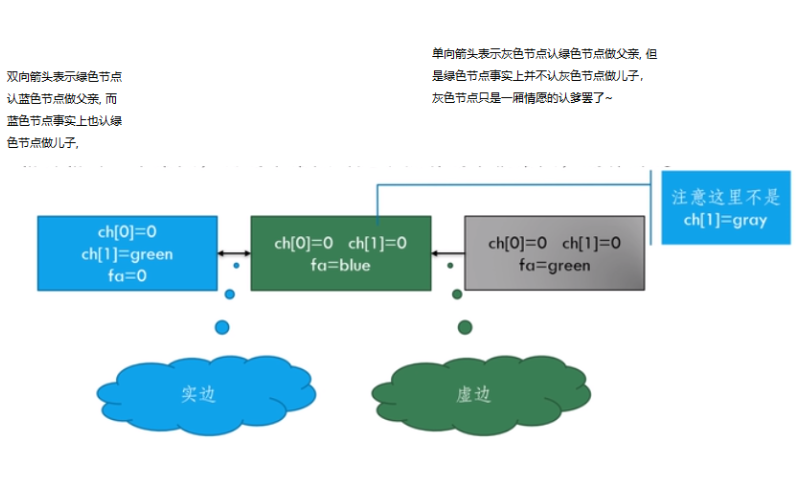
所以实边可以理解为正常的splay中的父子节点存储方式（即图1中的蓝色、绿色节点就是splay上的一对父子节点），所谓正常指的是父节点的ch[0]或者ch[1]指向子节点， 而子节点的fa指向父节点. 也就是图1中蓝色节点和绿色节点之间的双向箭头边.

虚边可以理解为splay的一个根节点（图1中的灰色节点）的fa指针指向一个节点（图1中的绿色节点），但是这个节点（图1的绿色节点）在splay上并没有一个儿子节点是该根节点（图1中的灰色节点）. 也就是图1中绿色节点和灰色节点之间的单向箭头边.

每棵splay的根节点都有一条虚边.

Link Cut Tree入门

image

但是注意，不论是实边还是虚边，连接的两个节点在同一棵原树上， 不同点是，实边连的两个节点在一棵splay（实链）中，虚边连接的两个节点不在一棵splay（实链）中.

下面逐个击破lct这种数据结构中的各种基本操作

约定: 除非特别说明，下面说将某个点x进行splay意味着将 x 伸展到x所在的splay的根节点位置

首先是lct中最基本且最重要的操作——access操作.

access

access(x): 用途将原树中从x到原树根节点的路径变成一根实链. 举个例子, 下图是一棵A为根节点的原树,

Link Cut Tree入门

image

access(N), 表示从要将原树中的路径 N->L->I->H->G->C->A变成一条实链. 我们假设图2的lct目前长图3的样子. 后面会发现，access(N)操作完成之后该lct的模样会发生变化.

Link Cut Tree入门

image

步骤:

  1. 将x进行splay，如果是第一次执行步骤1的话, 则将x的右儿子变成虚儿子
  2. 此时x已经是它所在的splay的根节点, 然后找到x的lct中的父节点fa, 则x到fa一定是lct中的虚边, 然后让fa进行splay , 然后将fa的右（实）儿子（即ch[1]）设置为x，则自动（因为fa只能有一个右儿子啊~）就将fa原本的右儿子（如果存在的话）变成虚儿子了. 形象的讲，就是儿子(x) 拜托老子（fa）去革命（splay），老子成功上位（splay到根）之后，就扶持儿子做实的右儿子而将原本的实的右儿子踢开变成虚儿子.
  3. 对fa（fa此时已是一棵splay的根节点）的父节点重复上述步骤.

ps: 这里多说一句, 既然虚儿子本质上并不是真的splay意义下的儿子（即它指向的父节点实际上并不承认有这么个儿子），所以就没有所谓的虚左儿子、虚右儿子之说了~

还是以上面图3为例看一下， 依旧考虑的是access(N)

首先我们对N进行 splay, 也就是将N在O、L、N三个节点组成的splay中进行伸展操作.

Link Cut Tree入门

image

也就是要对下面这棵splay的N节点进行伸展.

Link Cut Tree入门

image

（之字形）splay之后变成

Link Cut Tree入门

image

注意，上面的边都是实边. 因为我们是第一次执行步骤1，所以要将N的右儿子O变成虚儿子，也就是让N.ch[1] = 0 就可以了. 即变成下图的样子，注意画圈的边从图6中的双向箭头边（实边）变成了图7中的单向箭头边（虚边）

Link Cut Tree入门

image

注意，从上图的演变我们就能知道为什么步骤1中说——如果是第一次执行步骤1的话, 则就要将N的右儿子变成虚儿子. 因为N伸展之后，它的右儿子O是深度比它大的，而我们的目的仅仅是构造N到A的实链, N显然是该实链的底端节点，注意到实链的底端节点的深度是最大的，即N将是这根实链上深度最大的节点，所以不能把O也给拉进来. 所以自然要把O变成N的虚儿子.

然后我们继续, N因为新晋为splay的根节点， 所以自然是其父节点 I 的虚儿子，我们拜托 I 去splay一下，I所在的splay仅仅有 I、K 两个节点，splay之后显然 I 做根节点，K是其右儿子（因为 K 深度比 I 大），然后设置I的右儿子为N，则自然的就把I原本的右儿子K踢开变成了虚儿子了, 这一切画在了图8中.

Link Cut Tree入门

image

注意，和刚刚说的 为什么第一次执行步骤1的话就要将右儿子设置成0 道理是一样的，通过图8我们就能明白为什么要将I的右儿子设置成N——因为 N到 I 是虚边，所以 I 是原树中N到A所必须经过的节点， 即 I 一定要在N到A的实链上出现，而N的深度又是此实链上深度最深的——自然比 I 深, 所以 I 的splay意义下的右儿子要设置为N（毕竟splay关于深度形成bst嘛~）.

后面就是图8步骤的重复了.

Link Cut Tree入门

image

最后，我们伸展H的父节点A, A的右儿子设置为H（A原本的右儿子B就变成了虚儿子）. 就像下图10

Link Cut Tree入门

image

前面已经说了access(N)的目标是将原树中的路径 N->L->I->H->G->C->A 变成实链. 而实链就是恰好在一棵splay中的（类比于重剖中的一根重链就是在一棵线段子树中的）. 我们剥离出图10中的这棵splay

Link Cut Tree入门

image

根据lct中的splay是关于节点在原树中的深度形成bst的事实，深度大小依次为A<C<G<H<I<L<N

然后我们看看图2中原树是不是如此? 恰好如此！说明我们access(N)是成功的!

access的伪代码如下

inline void access(int x)
{
    for(re y = 0; x; x = fa[y = x]) 
    {
        splay(x); // x革命, x可以用图8中的I理解
        x.rc = y; // 革命成功后扶持y做右儿子,踢开原先的右儿子, y可以用图8中的N理解
        pushup(x); // splay的结构变了, 肯定要pushup的, 学过线段树的话很容易理解
    }
}

复制

有了上面的讲解, 伪代码很容易理解.

ps: 这里多说一句, 通过上面的access操作的图示，我们就不难发现，如果承认access是lct中重要的基本操作的话（下面就会发现，其他操作大量依赖access），那么使用splay来维护实链（bst）是极为自然的，因为当我们要access(N)的时候，如果N不是它所在的splay的根节点的话，我们就要将N变成它所在splay的根节点才行，为什么要变成其所在splay的根节点? 因为虚边是沟通不同splay之间的桥梁，而桥梁的一端必须是splay的根节点啊~ 而这种能将一棵树中的节点快速（摊还O(logn)）变为根节点的数据结构不就是splay或者fhqtreap了嘛~ 但是网上大佬说 fhqtreap 搞lct 容易被卡常.所以用splay来实现bst就是极为自然的了.

有了access之后，后面的操作就都比较简单了~

mkrt

mkrt(x) 就是给原树换根为x.

步骤:

  1. access(x)， 即打通x到原树根节点rt的路径为一条实链，所以x和rt就在同一棵splay中了（因为实链恰好就是一棵splay来维护的嘛~）. 而且因为x在实链的最底端，所以x的深度是实链中最大的, 所以x就是这棵splay的极右端点.
  2. x 进行splay, 即让x取代rt， 因为x是该实链中的深度最大的点, 所以x取代rt之后是没有右子树的（即x没有实的右儿子）.
  3. 翻转整棵splay

这里说的翻转就是二叉树翻转，即翻转rt为根二叉树的意味着下面的伪代码

void dfs(int rt)
{
    if(!rt)
    {
        return;
    }
    swap(rt.lc, rt.rc);
    dfs(rt.lc);
    dfs(rt.rc);
}

复制

为什么翻转整棵splay之后就达到了换根的目的呢?

还是画图. 图11进行第二步之后（即N splay 到A的位置）变成

Link Cut Tree入门

image

图12对应的实链就是图12的splay进行中序遍历的结果 A->C->G->H->I->L->N （深度单调增加），图12翻转之后变成（刚好和图12镜面对称）

Link Cut Tree入门

image

对应实链变化（就是图13的splay进行中序遍历的结果）为 N->L->I->H->G->C->A （深度单调增加）. 你看，N从原本实链上深度最深的节点变成了深度最浅的节点（原树的根节点不就是整棵原树中深度最浅的点吗?），更确切讲，实链的顺序完全反过来了——这不就实现原树换根了吗?

伪代码就很好理解了

inline void mkrt(int x)
{
    access(x);
    splay(x);
    rev(x);
}

复制

显然，rev操作要使用splay打懒标记的方法降低复杂度.

findrt

findrt(x) 的目的是找x在森林中的根节点（注意，不是找x所在splay的根节点哈）.

步骤

  1. access(x)
  2. splay(x)
  3. x所在splay的极左节点就是答案ans
  4. （血の教训）为了防止数据卡链, 还要splay(ans)

因为经过步骤1和步骤2, x已经成为其所在splay的根节点, 而且该splay没有右节点, 而x所在森林中的根节点就是x所在实链的顶端, 这是实链中深度最小的节点, 所以对应到splay中就是极左节点.

例如图12中，N所在splay的极左节点就是A，所以A就是N在森林中的根节点. 这是正确的.

伪代码很好理解

inline int findrt(int x)
{
    access(x);
    splay(x);
    while(x.lc)
    {
        pushdown(x); // 下推懒标记
        x = x.lc; // 一路向左
    }
    splay(x); // 防止数据卡链
    return x;
}

复制

关于步骤4的形象说明: 经过步骤1、步骤2，如果x所在splay蜕化成了一根链（毕竟splay并不保证绝对的平衡）

Link Cut Tree入门

image

则答案是ans, 如果数据比较毒瘤的一直询问你findrt(x)的话，则每次你都要经过漫长的上面findrt伪代码第五行的while循环. 这不就被卡了么? 所以最后要将ans splay一下. 下次要是还问findrt(x) 的话, 则O(1)时间就可以回答.

link

link(x, y)的目的是x和y之间连边.

步骤

  1. mkrt(x)
  2. 如果findrt(y) == x, 则x、y在同一棵原树上, 就别连了. 不然强行连边的话不就树中有环了么?
  3. 将x的lct意义下的父节点置为y，即像图15这般添加一条虚边即可（不必连实边，因为没有必要的情况下，不需要将x和y放在一根实链上）
Link Cut Tree入门

image

伪代码如下

inline void link(int x,int y)      
{
    mkrt(x);                     
    if(findrt(y) == x)
    {
        return;
    }
    x.fa = y; // 连虚边, 因为仅仅连的是虚边, 这条边在splay中并不实际存在而仅仅是在原树中实际存在, 所以splay的结构并没有变化, 所以并不需要pushup来维护splay
}

复制

cut

cut(x, y) 目的是断掉x和y之间的连边（实边），这是link(x, y)的逆操作. 同样要注意数据的合法性.

步骤:

  1. mkrt(x)
  2. 如果findrt(y) != x || y.fa != x || y.ch[0] != 0 那么直接return掉
  3. 断实边. 即将x.ch[1] = y.fa = 0
  4. pushup(x)

其中第二步是什么道理呢? findrt(y) != x 意味着x和y根本就不在一棵原树上，那自然是不能cut的. 那自然要return 掉, 所以我们现在假设findtr(y) == x成立. 然后我们注意到 findrt(y) 的最后一步是将 findrt(y) 的结果，也就是x splay到根（注意，经过findrt(y), 确切讲是经过 findrt 的第一步access之后，y和x已经在一条实链上了, 即已经在一棵splay中了）, 而x是原树的根节点啊~ 所以深度是最小的, 所以x被splay到根之后它只会有右节点. 兹麻里, y在x的右子树中, 那么什么情况下x和y之间不能进行cut呢? 无非就是下面两种使得x和y在原树上不相邻（不相邻自然不能cut）的情况

Link Cut Tree入门

image

情况1对应的就是 y.fa != x 情况2对应的就是 y.ch[0] != 0

伪代码就很好懂了

inline void cut(int x,int y) 
{
    mkrt(x); 
    if(findrt(y) ^ x || y.fa ^ x || y.ch[0]) 
    {
        return;
    }
    y.fa = x.ch[1] = 0; 
    pushup(x); // 因为x和y断了实边, splay的结构发生了变化, 所以要pushup维护splay
}

复制

split

split(x, y) 的目的是把 x 到 y的路径（所以前提肯定是x和y在同一棵树中, 题目的输入也保证这一点）变成一根实链.

步骤

  1. mkrt(x), 即先让x、y中的一个点变成所在树的根节点, 方便后续操作.
  2. access(y)，x和y之间的路径就变成了一根实链了，而且这根实链恰好通过一棵splay维护起来了.
  3. splay(y)，因为上一步的access(y)使得y成为xy之间的实链上深度最大的点, 所以将y splay到根节点，则新的splay就没有右儿子, 这样方便操作. 因为你想询问这条实链上的属性只需要访问y节点的属性就可以了.

伪代码就很好懂了

inline void split(int x,int y)
{
    mkrt(x);
    access(y);
    splay(y);
}

复制

至此, lct这种数据结构的基本操作都讲完了. 下面开始切代码.

//#include "stdafx.h"
//#define LOCAL
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#define re register int
#define ilv inline void
#define ili inline int
#define ilc inline char
#define swp(x, y) x^=y^=x^=y
namespace fastio
{
    const int BUF = 1 << 21;
    char fr[BUF], fw[BUF], *pr1 = fr, *pr2 = fr;
    int pw;

    ilc gc()
    {
        if (pr1 == pr2)
        {
            pr1 = fr;
            pr2 = fr + fread(pr1, 1, BUF, stdin);
            if (pr1 == pr2)
            {
                return EOF;
            }
        }
        return *pr1++;
    }

    ilv flush()
    {
        fwrite(fw, 1, pw, stdout);
        pw = 0;
    }

    ilv pc(char c)
    {
        if (pw >= BUF)
        {
            flush();
        }
        fw[pw++] = c;
    }


    ilv read(int &x)
    {
        x = 0;
        char c = gc();
        while(!isdigit(c))
        {
            c = gc();
        }
        while(isdigit(c))
        {
            x = (x << 3) + (x << 1) +(c ^ 48);
            c = gc();
        }
    }

    ilv write(int x)
    {
        if (x > 9)
        {
            write(x / 10);
        }
        pc(x % 10 + 48);
    }

    ilv writeln(int x)
    {
        write(x);
        pc(10);
    }

} using namespace fastio;
const int maxn = 1e5+5;
int n, m;
struct SplayNode
{
    int val, fa, ch[2], xr, lz;
} sp[maxn];

ili ntrt(int cur)
{
    int fa = sp[cur].fa;
    return sp[fa].ch[0] == cur || sp[fa].ch[1] == cur;
}

ili isrc(int cur, int fa)
{
    return sp[fa].ch[1] == cur;
}

ilv pushup(int cur)
{
    int lc = sp[cur].ch[0], rc = sp[cur].ch[1];
    sp[cur].xr = sp[lc].xr ^ sp[cur].val ^ sp[rc].xr;
}

ilv pushdown(int cur)
{
    int &lc = sp[cur].ch[0], &rc = sp[cur].ch[1];
    if (sp[cur].lz)
    {
        if (lc)
        {
            sp[lc].lz ^= 1;
        }
        if (rc)
        {
            sp[rc].lz ^= 1;
        }
        swp(lc, rc);
        sp[cur].lz = 0;
    }
}

ilv rotate(int cur)
{
    int fa = sp[cur].fa;
    int ga = sp[fa].fa;
    int t = isrc(cur, fa);
    int k = isrc(fa, ga);
    int chd = sp[cur].ch[t ^ 1];
    sp[fa].ch[t] = chd;
    if (chd)
    {
        sp[chd].fa = fa;
    }
    if (ntrt(fa))
    {
        sp[ga].ch[k] = cur;
    }
    sp[cur].fa = ga;
    sp[fa].fa = cur;
    sp[cur].ch[t ^ 1] = fa;
    pushup(fa);
    pushup(cur);
}

void pushdownall(int cur)
{
    if (ntrt(cur))
    {
        pushdownall(sp[cur].fa);
    }
    pushdown(cur);
}

ilv splay(int cur)
{
    pushdownall(cur);
    while(ntrt(cur))
    {
        int fa = sp[cur].fa;
        int ga = sp[fa].fa;
        int t = isrc(fa, ga);
        int k = isrc(cur, fa);
        if (ntrt(fa))
        {
            t ^ k ? rotate(cur) : rotate(fa);
        }
        rotate(cur);
    }
}

ilv access(int x)
{
    for (re y = 0; x; x = sp[y = x].fa)
    {
        splay(x);
        sp[x].ch[1] = y;
        pushup(x);
    }
}

ilv mkrt(int x)
{
    access(x);
    splay(x);
    sp[x].lz ^= 1;
}

ili findrt(int x)
{
    access(x);
    splay(x);
    while(sp[x].ch[0])
    {
        pushdown(x);
        x = sp[x].ch[0];
    }
    splay(x);
    return x;
}

ilv link(int x, int y)
{
    mkrt(x);
    if (findrt(y) == x)
    {
        return;
    }
    sp[x].fa = y;
}

ilv cut(int x,int y)
{
    mkrt(x);
    if (findrt(y) ^ x || sp[y].fa ^ x  || sp[y].ch[0])
    {
        return;
    }
    sp[y].fa = sp[x].ch[1] = 0;
    pushup(x);
}

ilv split(int x, int y)
{
    mkrt(x);
    access(y);
    splay(y);
}

signed main()
{
#ifdef LOCAL
    freopen("d:\\data.in", "r", stdin);
//  freopen("d:\\my.out", "w", stdout);
#endif
    read(n), read(m);
    for (re i = 1; i <= n; i++)
    {
        read(sp[i].val);
    }
    int op, x, y;
    while(m--)
    {
        read(op), read(x), read(y);
        switch(op)
        {
        case 0:
            split(x, y);
            writeln(sp[y].xr);
            break;
        case 1:
            link(x, y);
            break;
        case 2:
            cut(x, y);
            break;
        case 3:
            splay(x);
            sp[x].val = y;
            break;
        default:
            break;
        }
    }
    flush();
    return 0;
}

复制

ac情况

所属题目

P3690 【模板】Link Cut Tree （动态树）

评测状态

Accepted

评测分数

100

编程语言

C++

代码长度

3.72KB

用时

769ms

内存

10.06MB

小结

本文学习了 lct 这种处理动态树的数据结构，但是通过上面的学习，我们发现lct有一个东西处理不了——维护子树信息，因为我们知道，比如重链剖分可以处理子树（因为子树就在一棵线段子树上）或者树链信息，lct可以处理树链上的信息（本题就是这样）但是维护不了子树上的信息~ 这时候就需要更高级的数据结构——Top Tree.

后面再学习Top Tree~ 事实上，树剖除了删边操作之外都能搞（加边就是树剖+并查集）而且常数比lct小很多（因为lct的大量依赖splay操作，所以lct的常数比较大），所以树剖性能比lct高而且好写~ 所以能用树剖就用树剖哈~

上一篇: 行业分享-5G+智能电网承载需求分析5G+智能电网
下一篇: 【Pre-Training】XLNet：预训练最强，舍我其谁1.Introduction2.XLNet3.Experiments4.Conclusion5.Reference