2016年计算机联考真题——寻求最大子集和的差

概述

已知由n（n>=2）个正整数构成的集合A ，将其划分成两个不相交的子集A1和A2，元素个数分别为n1和n2，A1和A2中元素之和分别为S1和S2。设计一个尽可能高效的划分算法，满足|n1-n2|最小且|S1-S2|最大。要求：

1）给出算法的基本设计思想。

2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

3）说明你所设计算法的平均时间复杂度和空间复杂度。

算法思想

根据快速排序的思想，把找到最佳的划分，把最小的[n/2]个数放到A1，其余的数放到A2。分组结果即为题意所求。

算法步骤：

1）若i=[n/2]，则划分结束。

2）若i<[n/2]，则枢轴及之前的所有元素均属于A1，继续对i之后的元素进行划分。

3）若i>[n/2]，则枢轴及之后的所有元素均属于A2，继续对i之前的元素进行划分。

基于该设计思想，毋须堆全部元素进行排序，其平均时间复杂度为O(n),空间复杂度为O(1)。

全部代码

#include <iostream>
#include <cstdlib>
using namespace std;

//初始化数组 
void SetArray(int* data,int size)
{
    //srand(time(0));
    cout<<"随机初始化"<<size<<"个数"<<endl;
    for(int i = 0 ; i < size ; i++){
        data[i] =rand()%100+1;
    }
}

void Print(int* data ,int size)
{
    for(int i = 0 ; i < size ; i++){
        cout<<data[i]<<" "; 
    }
    cout<<endl;
}

//交换函数 
void Swap(int* a ,int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

int FindMax(int* data,int size)
{
    int low = 0,high = size-1;
    int low0 = 0,high0 = size-1;
    int k = size/2;
    bool flag = true;
    while(flag){
        int pivot = data[low];      //确定枢纽 
        while(low < high){
            //找到右边第一个比枢纽小的数 
            while(low < high && data[high] > pivot){
                high--;
            }
            if(low != high){//如果还划分没有结束 
                data[low] = data[high];
            }
            //找到左边第一个比枢纽大的数 
            while(low < high && data[low] < pivot){
                low++;
            }
            if(low != high){//如果还划分没有结束 
                data[high] = data[low];
            }
            data[low] = pivot;//把枢纽放到合适的位置
            if(low == k-1){//如果low刚好是中间位置 
                flag = false;
            }else if(low < k-1){//现在枢纽位置小于中间位置 
                low0 = low++;//说明前low个数是已经是最小的了 
                high = high0;
            }else{
                high0 = high--;//说明后high个数是已经是最大的了
                low = low0;
            } 
        }
    }
    int s1 = 0,s2 = 0;
    for(int i = 0 ; i < k ; i++){
        s1 += data[i];
    }
    for(int i = k ; i < size ; i++){
        s2 += data[i];
    }
    return s2-s1;
 } 

int main()
{
    cout<<"请输入数组长度:"<<endl;
    int size,*data;
    cin>>size; 
    data = new int[size];

    SetArray(data,size);
    int max = FindMax(data,size);
    cout<<"数组为："<<endl;
    Print(data,size); 
    cout<<"划分枢纽为："<<endl;
    cout<<data[size/2];
    cout<<"划分结果为："<<endl;
    Print(data,size/2);
    Print(data+size/2,size-size/2); 
    cout<<"最大子集和的差为：";
    cout<<max;

    return 0;
 }            

复制

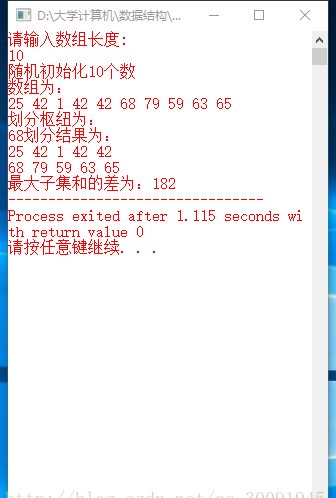
截图为：