最小生成树之普利姆（prim）算法的python实现

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索得到最小生成树。最小生成树即在一个带权连通图中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。

算法思路

利用字典建立图

以字典的形式建立加权连通图，通常以各顶点为字典的键，与该顶点所能连通的其余顶点再次构成一个子字典。这个子字典的键为所能连通的顶点，值为这个有向边的权重。这个子字典则构成了一个完整的值。

例如以下加权连通图：

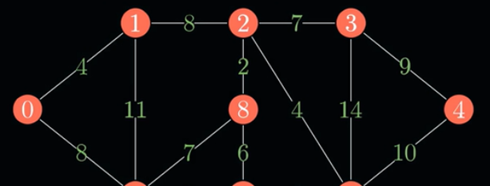
可表示为：

graph = {

            0: {1: 4, 7: 8},

            1: {2: 8, 7: 11},

            2: {8: 2, 5: 4, 3: 7},

            3: {4: 9, 5: 14},

            4: {5: 10},

            5: {6: 2},

            6: {7: 1, 8: 6},

            7: {8: 7}

        }           

将所有边放入同一个列表中

将所有边以三元组（始点，终点，权值）的形式放入一个列表中。

def init_edges(graph):

    edges = []

    for i in graph.keys():

        for j in graph[i].keys():

            edges.append((i,j,graph[i][j]))

return edges

           

前期准备

随机选择一个顶点加入到seen列表中，用来表示已经遇到过的顶点。

choice表示构建最小生成树时所有被选上的边，初始为空列表。

seen_edge表示所有已经碰到过的边，prim主要对这个列表进行处理，初始时为空列表。

主体循环部分

1. 判断已遇到过的顶点数量和总顶点数量的关系，当已遇到过的顶点数量少于总顶点数量时，说明还没有成功构造出含所有顶点的最小生成树，于是进入循环。
2. 每次循环都会将刚刚遇到过的顶点所能连接的边全部加入到seen_edge列表中，然后将seen_edge按权重进行由大到小的排序。
3. 如果seen_edge中权值最小的边的终点不在seen列表中，则将该终点加入到seen列表中，同时将这个边加入到choice列表中，随后将该边从seen_edge列表中删除，然后回到第1步。如果seen_edge中权值最小的边的终点已经在seen列表中，则不再考虑这条边，删除并继续找此时seen_edge中权值最小的边。
4. 步骤一无法进行下去后，返回的choice列表即为构建出最小生成树所需要的全部边。

graph = {
            0: {1: 4, 7: 8},
            1: {2: 8, 7: 11},
            2: {8: 2, 5: 4, 3: 7},
            3: {4: 9, 5: 14},
            4: {5: 10},
            5: {6: 2},
            6: {7: 1, 8: 6},
            7: {8: 7}
        }

def init_edges(graph):
    edges = []
    for i in graph.keys():
        for j in graph[i].keys():
            edges.append((i,j,graph[i][j]))
    return edges

def prim(graph):
    seen = [list(graph.keys())[0]]
    choice = []
    edges = init_edges(graph)
    seen_edge = []
    
    while len(seen) <= len(graph.keys()):
        for i in edges:
            if i[0] == seen[-1]:
                seen_edge.append(i)
        seen_edge.sort(key = lambda x:x[-1],reverse = True)
        while 1:
            if seen_edge[-1][1] not in seen:
                seen.append(seen_edge[-1][1])
                choice.append(seen_edge.pop())
                break
            else:
                seen_edge.pop()
        
                
        
    return choice

choice = prim(graph)