【算法入门08】青蛙跳台阶

核心考点：场景转化模型，模型提取解法，简单dp，fib

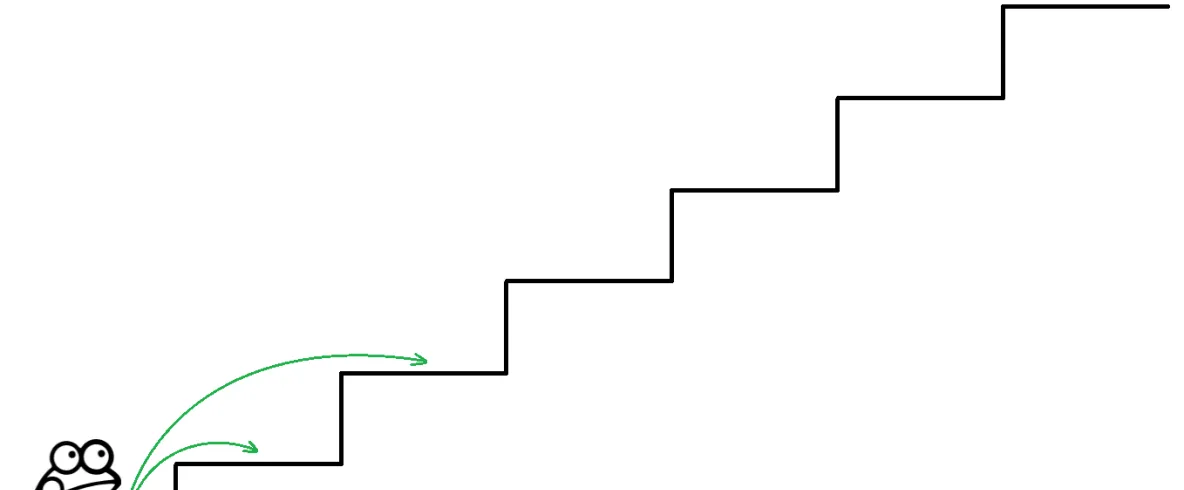
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求青蛙跳上一个n级的台阶共有多少种跳法（先后次序不同算不同的结果）。

解析：

对于这道题目，我们若是使用正向思维去思考，那这道题会变得非常困难，这时我们可以考虑使用逆向思维。

既然青蛙最终会到达第n级台阶，那青蛙必定是从第n-1级台阶或是第n-2级台阶跳到第n级台阶的。

也就是说青蛙跳到第n级台阶的总跳法数，等于青蛙跳到第n-1级台阶的总跳法数和青蛙跳到第n-2级台阶的总跳法数之和，即。

当然，我们不能让这个公式一直往前推，总得给它一个尽头，我们很容易得到青蛙跳到第0级台阶的总跳法数，和青蛙跳到第1级台阶的总跳法数：

• ，青蛙跳到第0级台阶的跳法只有一种，那就是不跳。
• ，青蛙跳到第1级台阶的跳法也只有一种，那就是从第0级台阶直接跳到第1级台阶。

这时代码也就出来了，我们可以使用递归来解决该问题：

//递归
class Solution {
public:
  int jumpFloor(int number) {
    if (number == 0 || number == 1) //f(0)=1, f(1)=1
      return 1;
    return jumpFloor(number - 1) + jumpFloor(number - 2); //f(n)=f(n-1)+f(n-2)
  }
};      

//动规
class Solution {
public:
  int jumpFloor(int number) {
    if (number == 0 || number == 1) //f(0)=1, f(1)=1
      return 1;
    int first = 1; //f(0)=1
    int second = 1; //f(1)=1
    int third = 0;
    while (number > 1) //进行number-1次计算
    {
      //f(n)=f(n-1)+f(n-2)
      third = first + second;
      first = second;
      second = third;
      number--;
    }
    return third;
  }
};