数据结构与算法之美-9 二叉树红黑树 [MD]

博文地址

我的GitHub	我的博客	我的微信	我的邮箱
baiqiantao		bqt20094	[email protected]

- 25 | 红黑树（上）：为什么工程中都用红黑树这种二叉树？
  - 平衡二叉查找树
  - 红黑树的定义
  - 为什么说红黑树是“近似平衡”的？
  - 解答开篇
  - 三种动态数据结构
- 26 | 红黑树（下）：掌握这些技巧，你也可以实现一个红黑树
  - 实现红黑树的基本思想
  - 插入操作的平衡调整
  - 删除操作的平衡调整
    - 针对删除节点初步调整
    - 针对关注节点进行二次调整
  - 内容小结
- 27 | 递归树：如何借助树来求解递归算法的时间复杂度？
  - 递归树
  - 归并排序
  - 快速排序
  - 斐波那契数列
  - 全排列

平衡二叉树 ：二叉树中任意一个节点的左右子树的 高度相差不能大于 1 。
平衡二叉查找树 ：除了满足上面平衡二叉树的定义，还满足二叉查找树的特点。

最先被发明的平衡二叉查找树是

AVL

树，它严格符合

平衡二叉查找树

的定义，即任何节点的左右子树高度相差不超过 1，是一种高度平衡的二叉查找树。但是很多平衡二叉查找树其实并没有

严格符合

上面的定义，比如下面要讲的红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。

发明平衡二叉查找树这类数据结构的初衷是，解决普通二叉查找树在

频繁的插入、删除

等动态更新的情况下，出现

时间复杂度退化

的问题。

平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

所以，只要一个平衡二叉查找树的高度不比

logn

大很多，尽管它不严格符合平衡二叉查找树的定义，但仍然是一个合格的平衡二叉查找树。

平衡二叉查找树其实有很多，比如，Splay Tree（伸展树）、Treap（树堆）等，但是提到平衡二叉查找树，听到的基本都是红黑树。它的出镜率甚至要高于“平衡二叉查找树”这几个字，有时候，我们甚至默认平衡二叉查找树就是红黑树。

红黑树的英文是

Red-Black Tree

，简称

R-B Tree

，它是一种

不严格

的平衡二叉查找树。

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

根节点是黑色的
每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据
- 这一条主要是为了简化红黑树的代码实现而设置的
- 下面在画图和讲解的时候，会将黑色的、空的叶子节点都省略掉
任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的
每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点

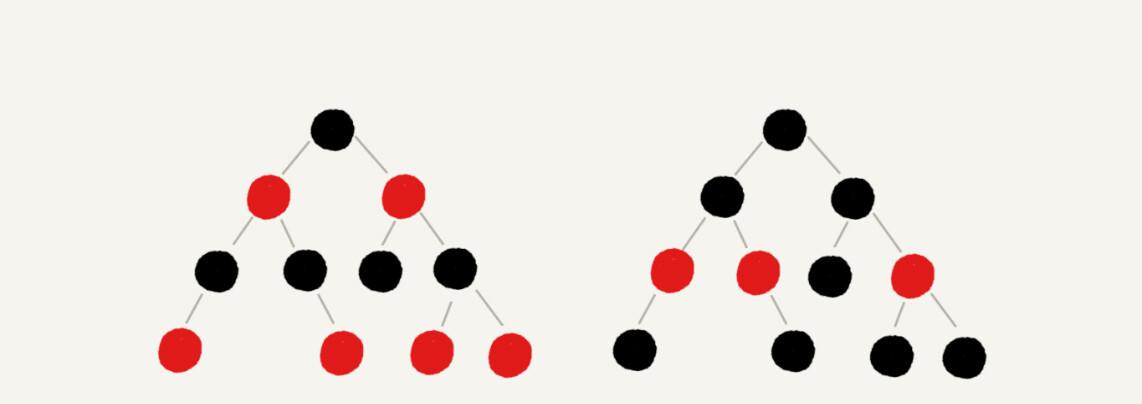
平衡二叉查找树的初衷是为了解决二叉查找树因为动态更新导致的性能退化问题。所以，“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化得太严重。

一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是

logn

，所以如果要证明红黑树是近似平衡的，只需要分析红黑树的高度是否比较稳定地趋近

logn

就好了。

后面省略若干内容......

前面提到的 Treap、Splay Tree，绝大部分情况下，它们操作的效率都很高，但是也

无法避免极端情况下时间复杂度的退化

。尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用。

AVL 树是一种

高度平衡

的二叉树，所以查找的效率非常高，但是，有利就有弊，AVL 树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用 AVL 树的代价就有点高了。

红黑树只是做到了

近似平衡

，并不是严格的平衡，所以在维护平衡的成本上，要比 AVL 树要低。所以，红黑树的插入、删除、查找各种操作性能都比较

稳定

，时间复杂度都是

O(logn)

。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，更倾向于这种

性能稳定

支持动态的数据插入、删除、查找操作的动态数据结构：

散列表：插入删除查找都是 O(1) ，是最常用的，但其缺点是不能顺序遍历以及扩容缩容的性能损耗。适用于那些不需要顺序遍历，数据更新不那么频繁的。
跳表：插入删除查找都是 O(logn) ，并且能顺序遍历。缺点是空间复杂度 O(n) 。适用于不那么在意内存空间的，其顺序遍历和区间查找非常方便。
红黑树：插入删除查找都是 O(logn) ，中序遍历即是顺序遍历，稳定。缺点是难以实现，去查找不方便。其实跳表更佳，但红黑树已经用于很多地方了。

实际上，魔方的复原解法是有固定算法的：遇到哪几面是什么样子，对应就怎么转几下。你只要跟着这个复原步骤，就肯定能将魔方复原。

红黑树的平衡过程跟魔方复原非常神似，大致过程就是：遇到什么样的节点排布，我们就对应怎么去调整。只要按照这些固定的调整规则来操作，就能将一个非平衡的红黑树调整成平衡的。

左旋（rotate left）：围绕某个节点的左旋
右旋（rotate right）：围绕某个节点的右旋

下图中的 a，b，r 表示子树，可以为空

红黑树规定，插入的节点必须是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。所以，关于插入操作的平衡调整，有这样两种非常好处理特殊情况：

如果插入节点的父节点是 黑色 的，那我们什么都不用做，它仍然满足红黑树的定义
如果插入的节点是 根节点 ，那我们直接改变它的颜色，把它变成黑色就可以了

除此之外，其他情况都会违背红黑树的定义，于是我们就需要进行调整，调整的过程包含两种基础的操作：

左右旋转

和

改变颜色

红黑树的平衡调整过程是一个

迭代

的过程。我们把正在处理的节点叫做

关注节点

。关注节点会随着不停地迭代处理，而不断发生变化。最开始的关注节点就是新插入的节点。

新节点插入之后，如果红黑树的平衡被打破，那一般会有下面三种情况。我们只需要根据每种情况的特点，不停地调整，就可以让红黑树继续符合定义，也就是继续保持平衡。

为了简化描述，我把父节点的兄弟节点叫做

叔叔节点

，父节点的父节点叫做

祖父节点

CASE 1：如果关注节点是 a，它的叔叔节点 d 是红色

我们就依次执行下面的操作：

将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色
将关注节点 a 的祖父节点 c 的颜色设置成红色
关注节点变成 a 的祖父节点 c
跳到 CASE 2 或者 CASE 3

CASE 2：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点

关注节点变成节点 a 的父节点 b
围绕新的关注节点 b 左旋
跳到 CASE 3

CASE 3：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点

围绕关注节点 a 的祖父节点 c 右旋
将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换
调整结束

红黑树插入操作的平衡调整还不是很难，但是它的删除操作的平衡调整相对就要难多了。不过原理都是类似的，我们依旧只需要根据关注节点与周围节点的排布特点，按照一定的规则去调整就行了。

删除操作的平衡调整分为两步，第一步是

针对删除节点初步调整

。初步调整只是保证整棵红黑树在一个节点删除之后，仍然满足最后一条定义的要求，也就是说，每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；第二步是

针对关注节点进行二次调整

，让它满足红黑树的第三条定义，即不存在相邻的两个红色节点。

这里需要注意一下，红黑树的定义中“只包含红色节点和黑色节点”，经过初步调整之后，为了保证满足红黑树定义的最后一条要求，有些节点会被标记成两种颜色，“红 - 黑”或者“黑 - 黑”。如果一个节点被标记为了“黑 - 黑”，那在计算黑色节点个数的时候，要算成两个黑色节点。

在下面的讲解中，如果一个节点既可以是红色，也可以是黑色，在画图的时候，我会用一半红色一半黑色来表示。如果一个节点是“红 - 黑”或者“黑 - 黑”，我会用左上角的一个小黑点来表示额外的黑色。

CASE 1：如果要删除的节点是 a，它只有一个子节点 b

那我们就依次进行下面的操作：

删除节点 a，并且把节点 b 替换到节点 a 的位置，这一部分操作跟普通的二叉查找树的删除操作一样
节点 a 只能是黑色，节点 b 也只能是红色，其他情况均不符合红黑树的定义。这种情况下，我们把节点 b 改为黑色
调整结束，不需要进行二次调整

CASE 2：如果要删除的节点 a 有两个非空子节点，并且它的后继节点就是节点 a 的右子节点 c

我们就依次进行下面的操作：

如果节点 a 的后继节点就是右子节点 c，那右子节点 c 肯定没有左子树。我们把节点 a 删除，并且将节点 c 替换到节点 a 的位置。这一部分操作跟普通的二叉查找树的删除操作无异
然后把节点 c 的颜色设置为跟节点 a 相同的颜色
如果节点 c 是黑色，为了不违反红黑树的最后一条定义，我们给节点 c 的右子节点 d 多加一个黑色，这个时候节点 d 就成了“红 - 黑”或者“黑 - 黑”
这个时候，关注节点变成了节点 d，第二步的调整操作就会针对关注节点来做

CASE 3：如果要删除的是节点 a，它有两个非空子节点，并且节点 a 的后继节点不是右子节点

找到后继节点 d，并将它删除，删除后继节点 d 的过程参照 CASE 1
将节点 a 替换成后继节点 d
把节点 d 的颜色设置为跟节点 a 相同的颜色
如果节点 d 是黑色，为了不违反红黑树的最后一条定义，我们给节点 d 的右子节点 c 多加一个黑色，这个时候节点 c 就成了“红 - 黑”或者“黑 - 黑”
这个时候，关注节点变成了节点 c，第二步的调整操作就会针对关注节点来做

经过初步调整之后，关注节点变成了“红 - 黑”或者“黑 - 黑”节点。针对这个关注节点，我们再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。

CASE 1：如果关注节点是 a，它的兄弟节点 c 是红色的

围绕关注节点 a 的父节点 b 左旋
关注节点 a 的父节点 b 和祖父节点 c 交换颜色
关注节点不变
继续从四种情况中选择适合的规则来调整

CASE 2：如果关注节点是 a，它的兄弟节点 c 是黑色的，并且节点 c 的左右子节点 d、e 都是黑色的

将关注节点 a 的兄弟节点 c 的颜色变成红色
从关注节点 a 中去掉一个黑色，这个时候节点 a 就是单纯的红色或者黑色
给关注节点 a 的父节点 b 添加一个黑色，这个时候节点 b 就变成了“红 - 黑”或者“黑 - 黑”
关注节点从 a 变成其父节点 b
继续从四种情况中选择符合的规则来调整

CASE 3：如果关注节点是 a，它的兄弟节点 c 是黑色，c 的左子节点 d 是红色，c 的右子节点 e 是黑色

围绕关注节点 a 的兄弟节点 c 右旋
节点 c 和节点 d 交换颜色
跳转到 CASE 4，继续调整

CASE 4：如果关注节点 a 的兄弟节点 c 是黑色的，并且 c 的右子节点是红色的

将关注节点 a 的兄弟节点 c 的颜色，跟关注节点 a 的父节点 b 设置成相同的颜色
将关注节点 a 的父节点 b 的颜色设置为黑色
从关注节点 a 中去掉一个黑色，节点 a 就变成了单纯的红色或者黑色
将关注节点 a 的叔叔节点 e 设置为黑色

为什么红黑树的定义中，要求叶子节点是黑色的空节点？

之所以有这么奇怪的要求，其实就是为了实现起来方便。只要满足这一条要求，那在任何时刻，红黑树的平衡操作都可以归结为我们刚刚讲的那几种情况。

假设红黑树的定义中不包含刚刚提到的那一条“叶子节点必须是黑色的空节点”，我们往一棵红黑树中插入一个数据，新插入节点的父节点也是红色的，两个红色的节点相邻，这个时候，红黑树的定义就被破坏了。那我们应该如何调整呢？

你会发现，这个时候，我们前面在讲插入时，三种情况下的平衡调整规则，没有一种是适用的。但是，如果我们把黑色的空节点都给它加上，变成下面这样，你会发现，它满足 CASE 2 了。

你可能会说，你可以调整一下平衡调整规则啊。比如把 CASE 2 改为“如果关注节点 a 的叔叔节点 b 是黑色或者不存在，a 是父节点的右子节点，就进行某某操作”。当然可以，但是这样的话规则就没有原来简洁了。

你可能还会说，这样给红黑树添加黑色的空的叶子节点，会不会比较浪费存储空间呢？答案是不会的。虽然我们在讲解或者画图的时候，每个黑色的、空的叶子节点都是独立画出来的。实际上，在具体实现的时候，我们只需要像下面这样，共用一个黑色的、空的叶子节点就行了。

很多人都认为红黑树很难学，其实主要原因是，他们都试图去记住它的

平衡调整策略

。实际上，你只需要

理解

这个调整过程就可以了，没有必要去记。

现在，我就来总结一下，如何比较轻松地看懂我今天讲的操作过程。

第一点，把红黑树的平衡调整的过程比作 魔方复原 ，不要过于深究这个算法的正确性。你只需要明白，只要 按照固定的操作步骤 ，保持插入、删除的过程，不破坏平衡树的定义就行了。
第二点，找准 关注节点 ，不要搞丢、搞错关注节点。因为每种操作规则，都是基于关注节点来做的，只有弄对了关注节点，才能对应到正确的操作规则中。在迭代的调整过程中，关注节点在不停地改变，所以，这个过程一定要注意，不要弄丢了关注节点。
第三点，插入操作的平衡调整比较简单，但是删除操作就比较复杂。针对删除操作，我们有两次调整，第一次是针对要删除的节点做初步调整，让调整后的红黑树继续满足第四条定义。但是这个时候，第三条定义就不满足了，有可能会存在两个红色节点相邻的情况。第二次调整就是解决这个问题，让红黑树不存在相邻的红色节点。

递归代码的

时间复杂度

分析起来很麻烦，前面我们讲过如何利用

递推公式

求解归并排序、快速排序的时间复杂度。但是，有些情况用递推公式的话，会涉及非常复杂的数学推导。今天，我们就来学习另外一种方法，借助

递归树

来分析递归算法的时间复杂度。

递归的思想就是将大问题分解为小问题来求解，然后再将小问题分解为小小问题。这样一层一层地分解，直到问题的数据规模被分解得足够小，不用继续递归分解为止。

如果我们把这个一层一层的

分解过程

画成图，它其实就是一棵树。我们给这棵树起一个名字，叫作

递归树

下图是

斐波那契数列

的递归树，节点里的数字表示数据的规模，一个节点的求解可以分解为左右子节点两个问题的求解。

利用递归树的时间复杂度分析方法并不难理解，关键还是在实战。

归并排序每次会将数据规模一分为二，现在我们就借助归并排序来看看如何用递归树，分析递归代码的时间复杂度。

我们把归并排序画成递归树，就是下面这个样子：

归并算法中比较耗时的是

归并操作

，也就是把两个

子数组

合并为

大数组

。从图中我们可以看出，

每一层归并操作消耗的时间总和是一样的

，跟要排序的数据规模有关，我们把每一层归并操作消耗的时间记作 n。

现在，我们只需要知道这棵树的高度 h，用高度 h 乘以每一层的时间消耗 n，就可以得到总的时间复杂度

O(n∗h)

从归并排序的原理和递归树可以看出来，归并排序递归树是一棵

满二叉树

，满二叉树的高度大约是

logn

，所以，归并排序递归实现的时间复杂度就是

O(nlogn)

为什么用递推公式来求解平均时间复杂度非常复杂？

快速排序在最好情况下，每次分区都能一分为二，这个时候用递推公式

T(n) = 2*T(n/2) + n

，很容易就能推导出时间复杂度是

O(nlogn)

。但是，我们并不可能每次分区都正好一分为二。

假设平均情况下，每次分区之后，两个分区的大小比例为

1:k

。当 k=9 时，用递推公式的方法来求解时间复杂度的话，递推公式就写成

T(n)=T(n/10) + T(9n/10) + n

这个公式可以推导出时间复杂度，但是推导过程非常复杂。

如果我们把递归分解的过程画成递归树，就是下面这个样子：

快速排序的过程中，每次分区都要遍历待分区区间的所有数据，所以，

每一层

分区操作所遍历的数据的个数之和就是 n。我们现在只要求出递归树的高度 h，这个快排过程遍历的数据个数就是

h∗n

，也就是说，时间复杂度就是

O(h∗n)

因为每次分区并不是均匀地一分为二，所以递归树并不是满二叉树。这样一个递归树的高度是多少呢？

我们知道，快速排序结束的条件就是待排序的小区间大小为 1，也就是说叶子节点里的数据规模是 1。从根节点 n 到叶子节点 1，递归树中最短的一个路径每次都乘以

1/10

，最长的一个路径每次都乘以

9/10

。通过计算，我们可以得到：

所以，遍历数据的个数总和就介于最短路径和最长路径之间，所以，当分区大小比例是

1:9

时，快速排序的时间复杂度仍然是

O(nlogn)

刚刚我们假设 k=9，那如果 k=99，也就是说，每次分区极其不平均，两个区间大小是

1:99

，这个时候的时间复杂度是多少呢？

我们可以类比上面 k=9 的分析过程。当 k=99 的时候，尽管底数变了，但是时间复杂度也仍然是

O(nlogn)

也就是说，对于 k 等于 9，99，甚至是 999，9999……，只要

k 的值不随 n 变化

，是一个事先确定的常量，那快排的时间复杂度就是

O(nlogn)

斐波那契数列的代码实现

int f(int n) {
  if (n == 1) return 1;
  if (n == 2) return 2;
  return f(n-1) + f(n-2);
}

把上面的递归代码画成递归树，就是下面这个样子：

这棵递归树的高度是多少呢？

f(n) 分解为

f(n−1)

f(n−2)

，每次数据规模都是 −1 或者 −2，所以，从根节点走到叶子节点，每条路径是长短不一的。如果每次都是 −1，那最长路径大约就是

；如果每次都是 −2，那最短路径大约就是

n/2

每次分解之后的合并操作只需要一次加法运算，我们把这次加法运算的时间消耗记作 1。所以，从上往下，第一层的总时间消耗是 1，第二层的总时间消耗是 2，第三层的总时间消耗就是

2^2

。依次类推，第 k 层的时间消耗就是

2^(k−1)

，那整个算法的总的时间消耗就是每一层时间消耗之和。

如果路径长度都为 n，那这个总和就是

2^n − 1

所以，这个算法的时间复杂度就介于

O(2^n)

O(2^n/2)

之间。

如何把 n 个数据的所有排列都找出来，这就是全排列的问题。

比如，1，2，3 这样 3 个数据，有下面这几种不同的排列：

1, 2, 3
1, 3, 2
2, 1, 3
2, 3, 1
3, 1, 2
3, 2, 1

如何编程打印一组数据的所有排列呢？这里就可以用递归来实现。

如果我们确定了最后一位数据，那就变成了求解剩下

n−1

个数据的排列问题。而最后一位数据可以是 n 个数据中的任意一个，因此它的取值就有 n 种情况。所以，n 个数据的全排列问题，就可以分解成 n 个

n−1

个数据的全排列的子问题。

递推公式：

假设数组中存储的是1，2， 3...n
f(1,2,...n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} + ... + {最后一位是n, f(n-1)}

// 调用方式：
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k表示要处理的子数组的数据个数
public void printPermutations(int[] data, int n, int k) {
  if (k == 1) {
    for (int i = 0; i < n; ++i) {
      System.out.print(data[i] + " ");
    }
    System.out.println();
  }

  for (int i = 0; i < k; ++i) {
    int tmp = data[i];
    data[i] = data[k-1];
    data[k-1] = tmp;

    printPermutations(data, n, k - 1);

    tmp = data[i];
    data[i] = data[k-1];
    data[k-1] = tmp;
  }
}

如果不用递归树分析方法，这个递归代码的时间复杂度会比较难分析。

首先，我们还是画出递归树。不过，现在的递归树已经不是标准的二叉树了。

第一层分解有 n 次交换操作，第二层有 n 个节点，每个节点分解需要

n−1

次交换，所以第二层总的交换次数是

n∗(n−1)

。第三层有

n∗(n−1)

个节点，每个节点分解需要

n−2

次交换，所以第三层总的交换次数是

n∗(n−1)∗(n−2)

以此类推，第 k 层总的交换次数就是

n∗(n−1)∗(n−2)∗...∗(n−k+1)

。最后一层的交换次数就是

n∗(n−1)∗(n−2)∗...∗2∗1

。每一层的交换次数之和就是总的交换次数。

n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1

有些代码的时间复杂度比较适合用 递推公式 来分析，比如归并排序、快速排序的最好情况时间复杂度
有些比较适合采用 递归树 来分析，比如快速排序的平均时间复杂度
有些可能两个都不怎么适合使用，比如二叉树的递归前中后序遍历

数据结构与算法之美-9 二叉树红黑树 [MD]

继续阅读

设计模式-组合模式（Composite Pattern）

推荐一款个人感觉比较好用的 JSON 格式化 chrome 插件-JSON-handle

HDU 5379 Mahjong tree

百度面试题-“盗梦空间”

bzoj 1010--玩具装箱toy

数据结构之递归实现

程序员的算法趣题Q09: 落单的男女1. 问题描述2. 解题分析3. 代码及测试4. 思考

时间复杂度及空间复杂度直白理解/快排/冒泡时间复杂度及空间复杂度直白理解/快排/冒泡

时间复杂度和空间复杂度时间复杂度空间复杂度推导过程

归并排序的时间复杂度

HDU 1207 汉诺塔II

递归经典整数划分问题

Redis：列表LPUSH、LPUSHX、RPUSH、RPUSHX、LPOP、RPOP命令介绍

PAT (Top Level) Practise 1007 Red-black Tree (35)

UVA 110 Meta-Loopless Sorts

UVA 620 Cellular Structure

数据结构与算法之美-9 二叉树 红黑树 [MD]

继续阅读

数据结构与算法之美-9 二叉树红黑树 [MD]