图论——倍增求LCA

LCA，最近公共祖先。

这是在树上的算法，但是为什么我们把它归为图论呢？

因为它对图论太重要了，其实，树也是图，是任意二节点只有一条路径的图。

我们来看一下LCA的栗子：

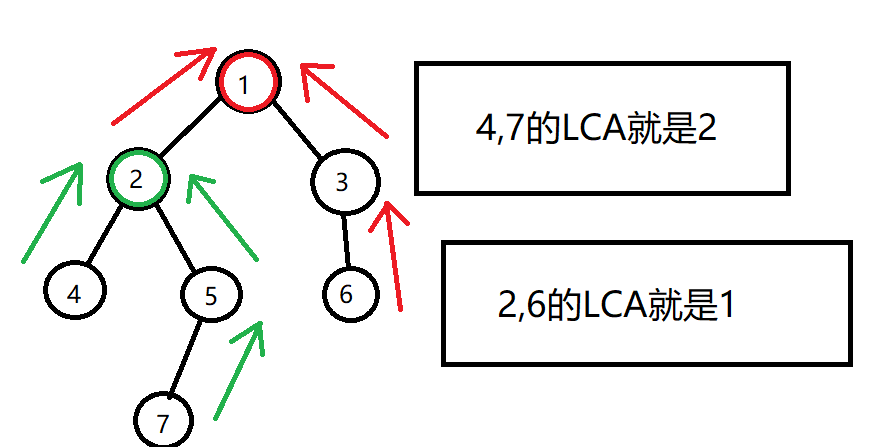
这就是LCA，很好理解吧！

那问题来了，怎么实现求两点的LCA呢？

其实很简单，用暴力法就可以了。先用树的DFS遍历求出树的深度，在一个一个向父节点搜索，找到一样的就是它们的LCA了！

简单粗暴吧！

大家可能会感到疑惑，真的有这么简单？

是的，是这么简单。来回顾一下问题：怎么实现求两点的LCA，DFS是能求，也好求。但是有一个缺点：太慢。

当我们的树的深度很大时，我们无法承受这巨大的复杂度，所以我们要想办法优化它。

我们先来看一下暴力解法的代码，并确保你理解了。

code

1 #include <bits/stdc++.h>
 2 #define MAXN 100005
 3 using namespace std;
 4 typedef long long ll;
 5 int v[MAXN];//标记节点是否被访问
 6 int fa[MAXN];//每个节点的父亲节点
 7 int depth[MAXN];//每个节点的深度
 8 vector<int>g[MAXN];//vector存树 
 9 void init()//初始化 
10 {
11     memset(v,0,sizeof(v));
12     memset(depth,0,sizeof(depth));
13     memset(fa,0,sizeof(fa));
14     for(int i=0;i<MAXN;i++)
15     {
16         g[i].clear();
17     }
18 }
19 void dfs(int s,int step)//DFS遍历 
20 {
21     depth[s]=step;
22     v[s]=1;
23     for(int i=0;i<g[s].size(); i++)
24     {
25         int k=g[s][i];
26         if(!v[k])
27         {
28             dfs(k,step+1);
29         }
30     }
31 }
32 int lca(int u,int v)
33 {
34     int fatheru=u;
35     int fatherv=v;
36     int depthu=depth[fatheru];
37     int depthv=depth[fatherv];
38     while(depthu<depthv)
39     {
40         fatherv=fa[fatherv];
41         depthv=depth[fatherv];
42     }
43     while(depthu>depthv)
44     {
45         fatheru=fa[fatheru];
46         depthu=depth[fatheru];
47     }
48     while(fatherv!=fatheru)
49     {
50         fatherv=fa[fatherv];
51         fatheru=fa[fatheru];
52     }
53     return fatherv;//暴力求LCA 
54 }
55 int main()
56 {
57     int n,m;
58     init();
59     cin>>n;
60     for(int i=1; i<n; i++)
61     {
62         int x,y;
63         cin>>x>>y;
64         g[x].push_back(y);
65         fa[y]=x;
66     }
67     int root=0;
68     for(int i=1;i<=n;i++)
69     {
70         if(fa[i]==0)
71             root = i;
72     }
73     dfs(root,1);
74     int u,v;
75     cin>>u>>v;
76     cout<<lca(u,v)<<endl;
77     return 0;
78 }      

额，有些长。

我们来讲讲如何~~优化~~

刚才，我们讲到，当树的深度太大时，复杂度很高，为什么呢？

因为每次跳一步太慢，若我们一次能往上走多步的话，时间复杂度会得到有效的控制。

这样的方法，我们叫树上倍增法。

这是一个运用广泛的算法，不仅仅用于求LCA..

我们用二维数组 f[ i ] [ k ]表示i的2^k倍祖先，就是i向上走2^k步到达的点，若它爆了深度，也就是它只向的节点不存在，就返回0.

f[ i ][ 0 ]表示 i 的 father 

对于任意的 i 属于 [ 1 ,  log n ],f [ i ][ k ]=f [ f[ x ][ k - 1] ][ k - 1 ];

这就是神奇的状态转移方程  ~QAQ~

蒟蒻：怎么涉及了DP？

是的，是涉及了DP，这也是它的难点之一。

 下面是代码：

1 const int SIZE=50010;
 2 int f[SIZE][20],d[SIZE],dist[SIZE];
 3 int ver[2*SIZE],Next[2*SIZE],edge[2*SIZE],head[SIZE];
 4 //采用图存储
 5 int T,n,m,tot=0,t;
 6 queue<int>q;
 7 void add(int x,int y,int z)
 8 {
 9     ver[++tot]=y;edge[tot]=z;Next[tot]=head[x];head[x]=tot;
10 }
11 void bfs()        //预处理 
12 {
13     q.push(1);
14     d[1]=1;
15     while(q.size())
16     {
17         int x=q.front();q.pop();
18         for(int i=head[x];i;i=Next[i])
19         {
20             int y=ver[i];
21             if(d[y])
22                 continue;
23             d[y]=d[x]+1;
24             dist[y]=dist[x]+edge[i];
25             f[y][0]=x;
26             for(int j=1;j<=t;j++)
27                 f[y][j]=f[f[y][j-1]][j-1];
28             q.push(y);
29         }
30     }
31 }
32 int lca(int x,int y)
33 {
34     if(d[x]>d[y])
35         swap(x,y);
36     for(int i=t;i>=0;i--)
37     {
38         if(d[f[i][i]]>=d[x])
39             y=f[y][i];
40     }
41     if(x==y)
42         return x;
43     for(int i=t;i>=0;i--)
44     {
45         if(f[x][i]!=f[y][i])
46         {
47             x=f[x][i];
48             y=f[y][i];
49         }
50     }
51     return f[x][0];
52 }      

可以看出，代码还是很长，这也是LCA让我们恼火的一点，记模板会很困难。还是理解了他们更好。

上面的代码用了图的链式前向星存法。

树也是一种图，所以这样保存是合理的。

bfs函数是预处理出每个节点的深度，在进行LCA算法。

明天就NOIP了，祝大家NOIP2018 rp++