前面我们说过 “不是所有的鸟都会飞”用谓词逻辑表示有两种方式:
B(x):x是一只鸟
F(x):x可以飞翔
这个语句就可以编码为:﹁(∀xB(x)→ F(x))
换而言之“只要是鸟就会飞,这种情况是不成立的”,上句话也可以编码为:∃ x(B(x) ∧﹁F(x) )
所以可知,在某些量词形式之间存在着语义的等价。本节就对其中的一些最常见和最常用的量词等价给出证明。
定理: 设Φ和Ψ是谓词逻辑公式,则具有下面的等价关系:
1.(a) ┐∀xΦ⇔∃x┐Φ
(b) ┐∃xΦ⇔∀x┐Φ
这两条比较好理解。
2.假设x在Ψ中不是自由的,那么:
(a)∀xΦ∧Ψ⇔∀x(Φ∧Ψ)
(b)∀xΦ∨Ψ⇔∀x(Φ∨Ψ)
(c)∃xΦ∧Ψ⇔∃x(Φ∧Ψ)
(d)∃xΦ∨Ψ⇔∃x(Φ∨Ψ)
(e)∀x(Ψ→Φ)⇔Ψ→∀xΦ
(f) ∃x(Φ→Ψ)⇔∀xΦ→Ψ
(g)∀x(Φ→Ψ)⇔∃xΦ→Ψ
(h)∃x(Ψ→Φ)⇔Ψ→∃xΦ
这里出现了一个概念:自由变量。这是一个和谓词逻辑公式语法树相关联的概念,还记得语法树的概念吗?
引入量词后,语法树变化并不大。下面是(∀x(P(x) ∧ Q(x))) -> (┐P(x) ∨ Q(y))的语法树:
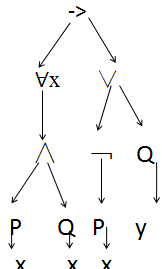
如果x是Φ的语法分析树中的一个叶结点,而且不存在从结点x到∀x或∃x的向上路径就称x的出现是自由的。否则,称x的出现是约束的。对∀xΦ或∃xΦ,我们称除去Φ的任何形如∀x或∃x的子公式的Φ分别是∀x或∃x的作用范围。那么你能说出上面这个语法树中哪个变量是自由的哪个是约束的吗?
3.(a)∀xΦ∧∀xΨ⇔∀x(Φ∧Ψ)
(b)∃xΦ∨∃xΨ⇔∃x(Φ∨Ψ)
4.(a)∀x∀yΦ⇔∀y∀xΦ
(b)∃x∃yΦ⇔∃y∃xΦ
看完这些等价公式,有没有感觉很自然。不过即使这样,我们也需要证明它们。
证明就需要用到量词的演算规则:
(1)等价关系规则
等价引入规则,不需要前提,一个变量总是和它自身相等
等价消去规则,使用了代换。说一下代换的概念:
给定变量x、项t和公式Φ,定义Φ[t/x]为用t代替Φ中的变量x的每个自由出现而得到的公式。
变量只是占位符,我们需用更具体的信息代替它,使其具有某种含义。从语法角度来讲,我们常用一个完全项t的语法分析树去代换叶结点x。由公式的定义,对x的代换只能是项,不会是谓词表达式,或者更复杂的公式,因为x只作为谓词符号的变量出现。切记在用t代换x时,必须避开那些受约束的变量x,因为它们处在某个∀x或∃x的作用范围,分别表示某些非特指的或所有的值。
此种变量代换也会产生意外副作用,如果t包含变量y,x在Φ中的自由出现处于Φ中∀x 或∃x的作用范围内。这种预料之外的变量捕捉是无论如何要避免的。
比如:考虑下图分析树公式Φ,并令t是f(y,y)。x在Φ中的两次出现全是自由的,出现在最左端的x可以被代换,因为它不在任何量词的作用范围之内。但是最右端叶结点x会引入一个t中的新变量y,它被∀y约束,所以f(y,y)对Φ中的x不是自由的。
(2)全称量词消去规则
全称量词引入规则
(3)存在量词引入规则
存在量词消去规则
这一篇说到这,其中概念很多,理解上也比较难。
下一篇需要用到刚说的量词证明规则和前面的命题演算规则对等价关系进行证明。