数据结构--堆排序

    通过学习优先队列和二叉堆，我们知道优先队列中队首的元素总是最大（最大堆）或者最小（最小堆）的元素，根据这个规律，如果我们把一系列无序的元素插入到优先队列中，然后再从优先队列中逐个删除元素，则删除元素的顺序是有序的。我们由此可以演变得出一种排序算法--堆排序。

    此处以最大堆来讨论，堆排序的实现分为2个阶段：构造堆阶段和下沉排序阶段；

构造堆阶段：通过下沉操作，将新添加到堆中的元素放到堆的根节点，然后与较大的子节点比较，如果小于子节点，则与子节点交换位置，使得较小的元素在堆中不断下沉，放入堆中合适的位置。

下沉排序阶段：构造堆完成后，堆的根节点存放的是最大的元素。排序阶段，每次将根节点元素与堆数组末尾元素交换位置，然后缩小堆的size，使得最大的元素从堆中剔除，放在数组末尾。然后通过下沉操作，使得根节点的新元素重新下沉到合适的位置。如此往复，直到堆中没有元素。此时，堆数组中的元素变为升序排列。

首先实现堆排序中需要的3个基本操作：

比较（less）：比较两个元素的大小，元素需要实现Comparable接口，从而可以被比较；

交换（exch）：交换两个元素在数组中的位置；

下沉（sink）：通过比较和交换，自上而下的移动元素，使其达到合适的位置；

    排序方法sort实际是对上面3个基本操作的组合，在构造堆阶段，通过sink操作构造好二叉堆。在排序阶段，通过exch操作将最大的元素排除到堆外，放到数组最末端，然后通过sink操作使堆重新变得有序。如此往复,直至堆中没有元素，此时数组即是有序的。基于最大堆的堆排序是升序的，反之，基于最小堆的堆排序是降序的。完整代码如下：

从上面代码可以看出，堆排序使用待排数组本身作为堆的存储结构，不占用额外的空间，因而属于内部排序。

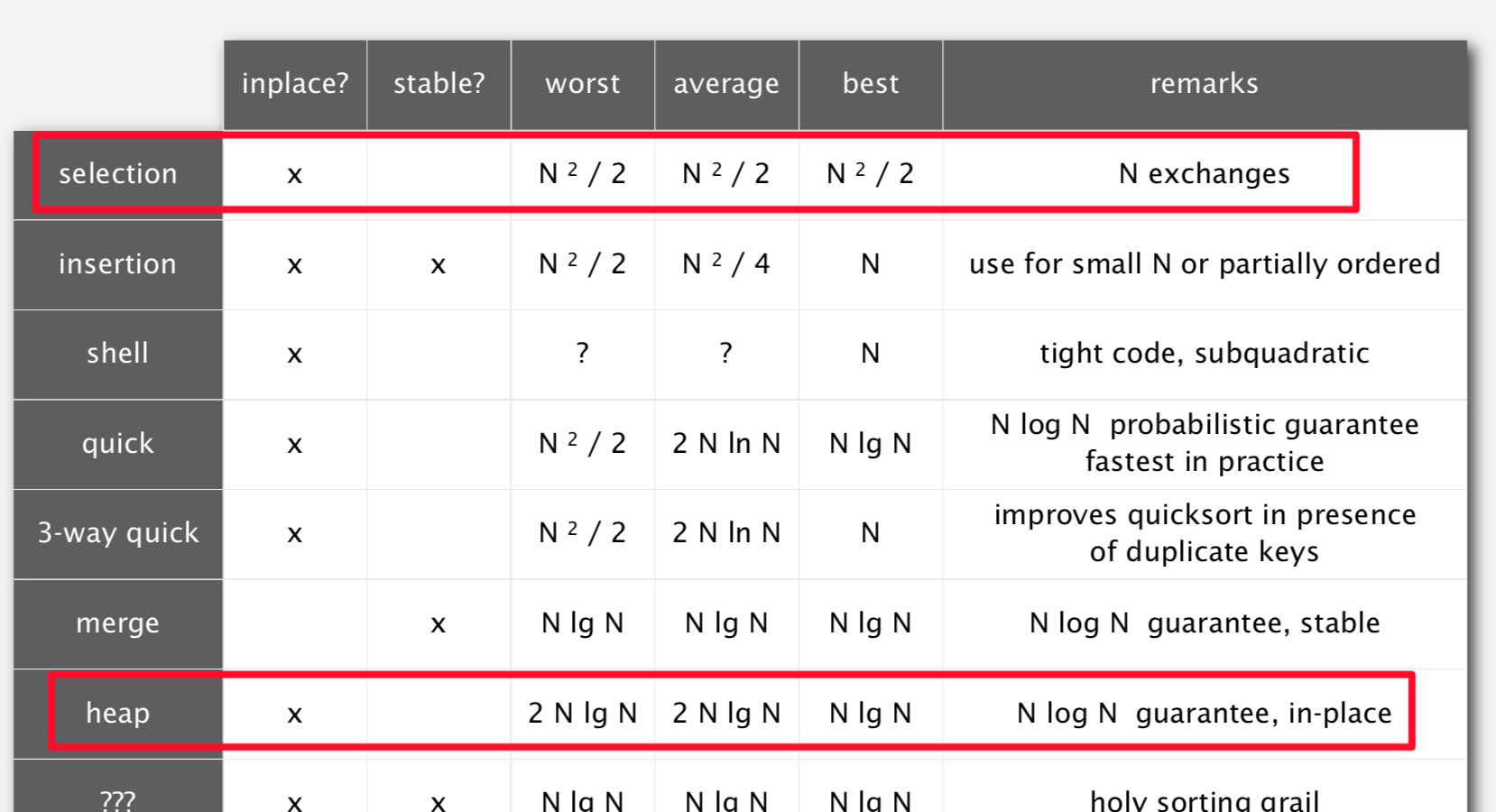
    堆排序的主要工作都是在下沉排序阶段完成的，每次从堆中删除最大的元素，然后放入到堆缩小后空出的空间中。这个过程和选择排序的过程类似，都是选择最大/最小的元素放到数组末尾，但相比于选择排序，堆排序在查找最大/最小元素的效率为$O(logN)$，高于选择排序的$O(N)$，从而提升了排序效率。

<a href="https://algs4.cs.princeton.edu/24pq/?spm=a2c4e.11153940.blogcont574087.13.4a774a58aGFL75">算法（第4版）2.4节-优先队列</a>

<a href="https://www.coursera.org/learn/algorithms-part1/home/week/4?spm=a2c4e.11153940.blogcont574087.14.4a774a58aGFL75">coursera算法视频课程</a>

<a href="https://www.toptal.com/developers/sorting-algorithms/heap-sort">堆排序示意动画</a>