声明:本程序设计参考象棋巫师源码(开发工具dephi 11,建议用delphi 10.3以上版本)。
这一章主要介绍置换表。本章目标:
实现置换表;
采用置换表走法、杀手走法等多种启发方式。
5.1 置换表
没有置换表,就称不上是完整的计算机博弈程序。在搜索过程中,某个搜索结果可能会出现这么多次,这浪费了很多时间。为避免重复搜索,保存搜索结果的表,就是置换表。由于哈希表的读写速度很快,通常置换表就由哈希表来实现。
置换表非常简单,以局面的 Zobrist Key mod HASH_SIZE 作为索引值。每个置换表项存储的内容无非就是:A. 深度,B. 标志,C. 分值,D. 最佳走法,E. Zobrist Lock 校验码。置换表结构:
置换表的处理函数也很传统——一个 ProbeHash 和一个 RecordHash 就足够了。
先说 RecordHash,即便采用深度优先的替换策略,RecordHash 也非常简单,在判断深度后,将 Hash 表项中的每个值填上就是了。
再看看 ProbeHash 是如何利用置换表信息的:
(1) 检查局面所对应的置换表项,如果 Zobrist Lock 校验码匹配,那么我们就认为命中(Hit)了;
(2) 是否能直接利用置换表中的结果,取决于两个因素:A. 深度是否达到要求,B. 非PV节点还需要考虑边界。
第二种情况是最好的(完全利用),ProbeHash 返回一个非 -MATE_VALUE 的值,这样就能不对该节点进行展开了。
如果仅仅符合第一种情况,那么该置换表项的信息仍旧是有意义的——它的最佳走法给了我们一定的启发(部分利用)。
5.2 杀棋分数调整
增加了置换表以后,杀棋分数要进行调整——置换表中的分值不能是距离根节点的杀棋分值,而是距离当前(置换表项)节点的分值。所以当分值接近杀棋分数时,ProbeHash 和 RecordHash 都要做细微的调整:
(1) 对于RecordHash:置换表项记录的杀棋步数 = 实际杀棋步数 - 置换表项距离根节点的步数;
(2) 对于ProbeHash:实际杀棋步数 = 置换表项记录的杀棋步数 + 置换表项距离根节点的步数。
5.3 杀手(Killer)走法
杀手走法就是兄弟节点中产生Beta截断的走法。根据国际象棋的经验,杀手走法产生截断的可能性极大。很显然,兄弟节点中的走法未必在当前节点下能走,所以在尝试杀手走法以前先要对它进行走法合理性的判断。在第二章里写过CanMove(走法是否合理)这个函数,这里它将大显身手。如果杀手走法确实产生截断了,那么后面耗时更多的 GenerateMove (生成所有走法)就可以不用执行了。
如何保存和获取“兄弟节点中产生截断的走法”呢?我们可以把这个问题简单化——距离根节点步数(nDistance)同样多的节点,彼此都称为“兄弟”节点,换句话说,亲兄弟、堂表兄弟以及关系更疏远的兄弟都称为“兄弟”。
我们可以把距离根节点的步数(nDistance)作为索引值,构造一个杀手走法表。每个杀手走法表项存有两个杀手走法,走法一比走法二优先:存一个走法时,走法二被走法一替换,走法一被新走法替换;取走法时,先取走法一,后取走法二。
5.4 优化走法顺序
利用各种信息渠道(如置换表、杀手走法、历史表等)来优化走法顺序的手段称为“启发”。第五章以前,我们只用历史表作启发,但从这个版本开始,我们采用了多种启发方式:
(1) 如果置换表中有过该局面的数据,但无法完全利用,那么多数情况下它是浅一层搜索中产生截断的走法,我们可以首先尝试它;
(2) 然后是两个杀手走法(如果其中某个杀手走法与置换表走法一样,那么可以跳过);
(3) 然后生成全部走法,按历史表排序,再依次搜索(可以排除置换表走法和两个杀手走法)。
这样,我们就可以构造一个状态机,来描述走法顺序的若干阶段:
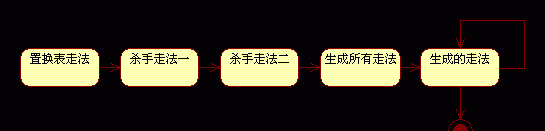
首先要定义走法结构:
其中Next方法就是状态机的实现:
提取置换表和保存置换表的代码如下:
SearchFull函数中生成所有走法,并逐一走这些走法被Next方法所替代:
以上程序未经充分测试,发现问题请及时反馈。
下一章将实现以下目标:
实现开局库;
实现PVS(主要变例搜索);
把根节点的搜索单独处理,增加搜索的随机性;
克服由长将引起的置换表的不稳定性。
其他未说明的内容请参阅源码注释,如有问题,敬请指出。
本章节源码百度云盘:
链接:中国象棋程序设计(五)置换表
提取码:1234