神奇,实现一门逻辑式语音竟然只需两页代码~
本文是本系列的完结篇。本系列前面的文章:
逻辑式编程语言极简实现(使用C#) - 1. 逻辑式编程语言介绍
逻辑式编程语言极简实现(使用C#) - 2. 一道逻辑题:谁是凶手
逻辑式编程语言极简实现(使用C#) - 3. 运行原理
下午,吃饱饭的老明和小皮,各拿着一杯刚买的咖啡回到会议室,开始了逻辑式编程语言的最后一课。
老明喝了一口咖啡,说:“你看咖啡机,是不是咖啡的列表。”
“啥?”小皮有点懵圈,“你说工厂的话还好理解,列表不太像。”
“每次点一下按钮,就相当于调用了一次next,出来一杯咖啡。而它本身并不包含咖啡,每一次都是现场磨豆冲出来的。这正是一个典型的惰性列表。”
“有点道理,但是这跟逻辑式编程语言解释器有什么关系呢?”
“这就是下面要说的流计算模式,它是实现分支遍历的核心技巧。”
下面先讲流计算模式,然后再讲替换求解的实现与分支遍历的实现。
老明在白板上写下“Stream”,说:“Stream最常见的用途是用来表示数量未知或者无穷的列表。在代码中怎么定义流呢?我们先来看看自然数,自然数是无穷的,那我们怎么定义自然数列呢?”
“这很显然,不就是0、1、2、3、4、5等等吧。”
老明鄙夷地看着小皮,说:“如果我是你的数学老师,那我肯定要罚你站在墙角数完所有自然数……想想数学归纳法!”
“哦哦,哎!数学这些乌漆嘛黑的知识总是喜欢偷偷溜走。自然数的定义简单来说(严谨的不会),由两部分组成:
(起点部分)0是自然数;
(递归部分)任意自然数加1也是自然数。
“这样我们根据第1部分,得到起点0;再根据第2部分,一直加1,依次得到1、2、3、4、5等自然数。”
“看来基础还是不错的。”老明微笑着点点头,然后开始进入正文……
从自然数的定义,我们可以得到启发,Stream的定义也是由两部分组成:
起点:第一个元素(非空流);
递归:一个无参函数,调用它会返回这个Stream去掉第一个元素后剩下部分组成的剩余Stream。
第2部分之所以是个函数,是为了获得惰性的效果,仅当需要时才计算剩余的Stream。
使用代码定义Stream如下:
其中<code>Substitution</code>是替换类,后面会讲到这个类的实现。
还需要定义一个空Stream,除了表示空以外,还用来作为有限Stream的结尾。空Stream是一个特殊的单例。
正常来讲,空Stream应该额外声明一个类型。这里偷了个懒。
特别的,还需要一个构造单元素的Stream的方法:
只有这些平凡的构造方法还看不出Stream的用处,接下来结合前面讲过的NMiniKanren运行原理,探索如何使用Stream来实现替换的遍历。
回顾一下<code>Any</code>的运行原理,<code>Any</code>的每个参数会各自返回一个Stream。这些Stream代表了各个参数包含的可能性。<code>Any</code>操作把所有可能性放在一起,也就是把这些Stream拼在一起组成一个长长的Stream。
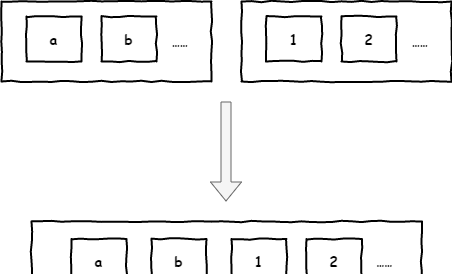
所以相应的,我们需要把两个Stream <code>s1</code>和<code>s2</code>拼接成一个“长”Stream的Append方法。
如何构造这个“长”Stream呢?
首先,如果<code>s1</code>是空Stream,那么拼接后的Stream显然就是<code>s2</code>。
否则,按照Stream定义,分两个部分进行构造:
第一个元素,显然就是<code>s1</code>的第一个元素;
剩余Stream,就是<code>s1</code>的剩余Stream,拼上<code>s2</code>,这里是个递归定义。
按照上面分析的构造方法,我们就能轻松地写下代码:
在这个实现中,<code>f</code>是尚未计算的<code>s2</code>。我们需要尽量推迟<code>s2</code>第一个元素的计算,因为推迟着推迟着可能就没了不用算了。在很多场景中,这个可以节省不必要的计算,甚至避免死循环(“这都是血泪教训。”老明捂脸)。
下面是一个<code>Any</code>与<code>Append</code>的例子:
<code>Anyi</code>和<code>Any</code>的区别只有顺序。<code>Anyi</code>使用交替的顺序。
所以相应的,我们需要一个方法,这个方法把两个Stream <code>s1</code>和<code>s2</code>中的元素交替地拼接组成一个“长”Stream。
首先,如果<code>s1</code>是空Stream,那么“长”Stream显然就是<code>s2</code>。
否则,分两部分构造:
第一个元素是<code>s1</code>的第一个元素;
这里和Append方法的区别是把<code>s1</code>和<code>s2</code>的位置调换了,剩余Stream是<code>s2</code>交替拼上<code>s1</code>的剩余Stream,同样是个递归定义。
代码如下:
这里使用惰性的<code>f</code>是非常必要的,因为我们不希望取剩余Stream的时候调用<code>GetRest</code>。
这个方法比较复杂,是对应到<code>All</code>运算中两两组合参数里的分支的过程。
不同于<code>Append</code>/<code>Interleave</code>作用在两个Stream上,<code>Bind</code>方法作用在一个Stream和一个Goal上。
为什么不是两个Stream呢?
前面已经分析过了,<code>k.All(g1, g2)</code>这个运算,是把<code>g2</code>蕴含的条件,追加到<code>g1</code>所包含的Stream中的每个替换里。
同时,<code>g2</code>是个函数。追加这个动作本身由<code>g2</code>表达。
举例来说,假设<code>st</code>是<code>g1</code>所包含的Stream中的一个替换。那么把<code>g2</code>蕴含的条件追加到<code>st</code>上,其结果为<code>g2(st)</code>。
正是因为<code>Bind</code>方法中需要有追加条件这个动作,所以<code>Bind</code>方法的第二个参数只能是既包含了条件内容,也包含了追加方法的Goal类型。
用记号<code>s1</code>表示<code>g1</code>所包含的Stream,<code>Bind</code>方法的作用就是把<code>g2</code>蕴含的条件追加到<code>s1</code>中的每个替换里。
首先,如果<code>s1</code>是个空Stream,那显然<code>Bind</code>的结果是空Stream。
否则,结果是<code>s1</code>的第一个元素追加<code>g2</code>,再拼上<code>s1</code>的剩余Stream <code>Bind</code> <code>g2</code>的结果。这仍是递归定义,不过是借助的<code>Append</code>方法进行Stream构造。
这个方法为什么叫<code>Bind</code>,因为取名废只好抄《The Reasoned Schemer》里的命名……
下面是一个<code>All</code>与<code>Bind</code>的例子:
对应<code>Alli</code>,交替版的<code>Bind</code>方法。代码实现不再多说,直接把<code>Bind</code>实现中的<code>Append</code>换成<code>Interleave</code>即可:
更多Stream的玩法,参见《计算机程序的构造和解释》(简称《SICP》)第三章。
构造目标时会用到替换里的方法,所以和上一篇顺序相反,先讲替换求解。
替换的定义为:
这是个单链表的结构。我们需要能在替换中追根溯源地查找未知量的值的方法(也就是将条件代入到未知量):
例如在替换<code>(x=1, q=(x y), y=x)</code>中,<code>Walk(q)</code>返回<code>(1 1)</code>。
注意替换结构里面,条件都是<code>未知量 = 值</code>的形式。但是在NMiniKanren代码中并非所有条件都是这种形式。所以在追加条件时,需要先将条件转化为<code>未知量 = 值</code>的形式。
追加条件时,不是简单的使用<code>Extend</code>方法,而是用<code>Unify</code>方法。<code>Unify</code>方法结合了<code>Extend</code>和代入消元法。它先将已有条件代入到新条件中,然后再把代入后的新条件转化为<code>未知量 = 值</code>的形式:
<code>Unify</code>方法实现了代入消元的第一遍代入(详情见上一篇)。<code>Unify</code>的全拼是unification,中文叫合一。
由于NMiniKanren的输出只有未知量<code>q</code>,所以第二遍代入的过程只需要查找<code>q</code>的值即可:
通过Stream的分析,我们知道,只要构造了目标,自然就实现了分支的遍历。
任何替换追加<code>Success</code>,相当于没追加,所以<code>k.Success</code>直接返回一个只包含上下文的Stream:
任何替换追加<code>Fail</code>,那它这辈子就完了,<code>k.Fail</code>直接返回空Stream
<code>k.Eq(v1, v2)</code>向上下文追加<code>v1 == v2</code>条件。
首先,使用<code>Unify</code>方法将<code>v1 == v2</code>条件扩展到上下文代表的替换。
若扩展后的替换出现矛盾,表示无解,返回空Stream。
否则返回只包含扩展后的替换的Stream。
首先,利用<code>Stream.Append</code>实现二目运算版本的<code>Or</code>:
然后扩展到多参数:
同理实现<code>Ori</code>和<code>Anyi</code>:
利用<code>Stream.Bind</code>实现二目版本的<code>And</code>:
同理实现<code>Andi</code>和<code>Alli</code>:
其中,<code>MapAndTake</code>方法取Stream的前n个(或所有)值,并map每一个值。
<code>Renumber</code>将自由变量替换成<code>_0</code>、<code>_1</code>……这类符号。
NMiniKanren的完整代码在这里:https://github.com/sKabYY/NMiniKanren
总结一下NMiniKanren的原理:
NMiniKanren代码描述的是一个Goal。Goal是一个替换到Stream的函数。
从NMiniKanren代码可以构建一张描述了条件关系的图。每条路径对应一个替换,使用流计算模式可以很巧妙地实现对所有路径的遍历。
使用代入消元法求解未知量。
另外NMiniKanren毕竟只是一门教学级的语言,实用上肯定一塌糊涂,说难听点也就是个玩具。我们学习的重点不在于NMiniKanren,而在于实现NMiniKanren的过程中所用到的技术和思想。掌握了这些方法后,可以根据自己的需要进行优化或扩展,或者将这些方法应用到其他问题上。
“神奇!”小皮瞪着眼睛摸摸脑袋,以前觉得宛若天书般的逻辑式编程语言就这么学完了,还包括了解释器的实现。
“认真学习了一天半的效果还是不错了。嘿嘿。”老明欣慰地拍了拍小皮的肩膀,微微笑道,“世上无难事,只怕有心人。恰好今天周五了,周末就来公司把这两天落下的工作补完吧。”
小皮:“???”
PS:最后,用《The Reasoned Schemer》里的两页实现镇楼。俗话说得好,C#只是恰饭,真正的快乐还得看Scheme/Lisp。