Medium
You are given a network of <code>n</code> nodes, labeled from <code>1</code> to <code>n</code>. You are also given <code>times</code>, a list of travel times as directed edges <code>times[i] = (ui, vi, wi)</code>, where <code>ui</code> is the source node, <code>vi</code> is the target node, and <code>wi</code> is the time it takes for a signal to travel from source to target.
We will send a signal from a given node <code>k</code>. Return the time it takes for all the <code>n</code> nodes to receive the signal. If it is impossible for all the <code>n</code> nodes to receive the signal, return <code>-1</code>.
Example 1:
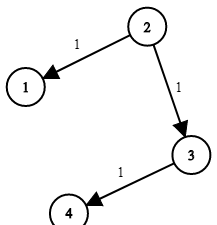
Example 2:
Example 3:
Constraints:
<code>1 <= k <= n <= 100</code>
<code>1 <= times.length <= 6000</code>
<code>times[i].length == 3</code>
<code>1 <= ui, vi <= n</code>
<code>ui != vi</code>
<code>0 <= wi <= 100</code>
All the pairs <code>(ui, vi)</code> are unique. (i.e., no multiple edges.)
There are <code>n</code> cities connected by some number of flights. You are given an array <code>flights</code> where <code>flights[i] = [fromi, toi, pricei]</code> indicates that there is a flight from city <code>fromi</code> to city <code>toi</code> with cost <code>pricei</code>.
You are also given three integers <code>src</code>, <code>dst</code>, and <code>k</code>, return the cheapest price from <code>src</code> to <code>dst</code> with at most <code>k</code> stops. If there is no such route, return <code>-1</code>.
<code>1 <= n <= 100</code>
<code>0 <= flights.length <= (n * (n - 1) / 2)</code>
<code>flights[i].length == 3</code>
<code>0 <= fromi, toi < n</code>
<code>fromi != toi</code>
<code>1 <= pricei <= 104</code>
There will not be any multiple flights between two cities.
<code>0 <= src, dst, k < n</code>
<code>src != dst</code>
BFS 这个解法会超时
类似dikjistra pq解法