详细的题目要求和实验资源可以到教材官网 或者 课程官网 获取。 本次实验难点在Part B的64 * 64部分,主要介绍这一部分。
<code>getopt</code>和<code>fscanf</code>系列库函数对于这次实验很重要,不太明白的可以<code>man</code>一下,或者参考这两篇文章:
Linux下getopt()函数的简单使用
C 库函数 - fscanf()
1.由于我们的模拟器必须适应不同的s, E, b,所以数据结构必须动态申请(malloc系列),注意初始化。
2.测试数据中以“I”开头的行是对指令缓存(i-cache)进行读写,我们编写的是数据缓存(d-cache),这些行直接忽略。
3.这次实验假设内存全部对齐,即数据不会跨越block,所以测试数据里面的数据大小也可以忽略。
4.为了使得评分程序正常运行,<code>main</code>函数最后需要加上:
5.建议把<code>-v</code>这个选项也实现了,这样自己debug的时候也方便一些。另外,可以先从规模小的测试数据开始,然后用大的。
1.这次实验只要求我们测试hit/miss/eviction的次数,并没有实际的数据存储 ,所以我们不用实现line中的block部分。
2.这次实验要求使用LRU(least recently used),即没有空模块(valid为0)时替换最早使用的那一个line。所以我们应该在line中实现一个能够记录当前line最后一次写入的时间参量,每次”写入“line的时候就更新一下该参量。(这一点csapp上没有详细说)
3.综上,结合书上对cache的描述,我们可以得到如下数据结构:
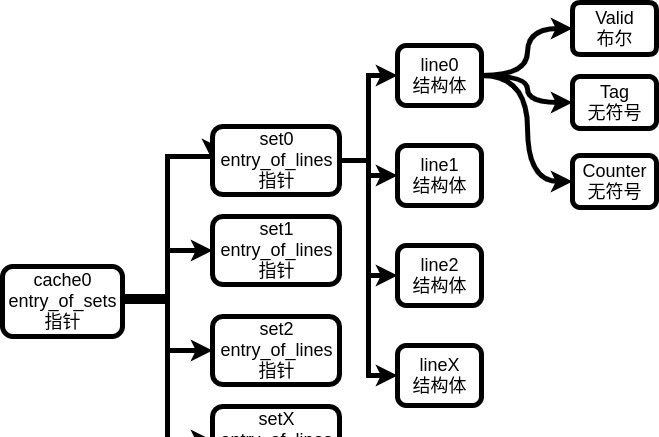
注意到cache(sets的入口)和set(lines的入口)都是用指针实现的,sets构成一个指针数组,因为它们不含任何数据,唯一的用处就是通过偏移量寻找到指定的line。
下面结合代码执行的顺序对我实现的程序进行解释,由于写了很多注释,就不详细的说了(我的sublime写不了中文,就用的英文注释的,语法有错还请指出)
更新:一航介绍了一个插件,可以解决Ubuntu下sublime中文输入的问题
--> sublime-text-imfix
头文件:
为什么要包含该头文件的原因在右侧注释中写出来了。由于我们实验使用的64位地址,所以将tag和set的索引用64位保存就足够了,我这里使用了C99中的固定长度类型uintN_t,可移植性好一些。另外要注意的是,C99必须包含unistd.h和getopt.h两个头文件才能正常使用<code>getopt</code> 。
宏定义:
我喜欢用_Bool+宏定义true和false,你也可以使用stdbool.h。
数据结构类型定义:
time_counter初始化的时候都是0,其值越大代表这个line最近刚刚被写入——我们不应该替换它——所以valid为0的line的time_counter一定也是0(最小值),因为他们连使用都没有被使用过,即我们一定会先替换valid为0的line,这符合书上的策略。
我将结果设计成了一个结构体,这样函数方便返回一些。(少用全局变量)
main函数的数据类型:
注释已经写的很清楚了,我解释一下help_message的写法,有的同学可能不知道C中字符串的写法:两个字符串中间只有空格,C编译器会自动将它们合并。例如:
那么test_string就会是“hello world”。
另外,在C中,一行写不下的时候可以使用\字符隔开,编译器会自动合并的。
main函数读取参数:
关于<code>getopt</code>的用法可以参考文章开头的文章;<code>perror</code>和<code>fopen</code>的用法请<code>man</code>一下,fopen失败后会设置errno的。
如果读取的参数中没有s或者b或者E或者文件,那么那他们将会是对应的初始值。
main函数调用函数并结束程序:
<code>InitializeCache</code>是用来动态申请数据结构的,<code>ReadAndTest</code>是本程序的核心,用来测试hit/miss/eviction的次数。另外不要忘记或者重复释放内存。下面分别介绍这三个函数。
我们首先根据S(set的数目)申请一个数组,该数组元素是lines的入口的指针。接着循环S次每次申请E个line数据结构,并让刚刚的指针数组的元素指向它们:
释放之前申请的内存:
不解释。
核心部分,测试hit/miss/eviction的次数:
如果命令是“L”或者“M”,我们就进入<code>HitMissEviction</code>一次判断其是否hit或者miss以及是否发生替换,如果是M就相当于一次“L”和一次“M”,需要进入<code>HitMissEviction</code>两次,其结果可能为两次hit,也可能为一次miss+(eviction)一次hit。我们在<code>ReadAndTest</code>里通过一些位运算找到对应的set(即entry_of_lines),然后以此作为参数调用<code>HitMissEviction</code> 判断到底是miss(有没有eviction)还是hit。
<code>HitMissEviction</code>里面需要注意的地方是时间参量的更新,我们既要找到最“老”的line,也要同时记住最“新”的line的时间参量(我这里是遍历搜索,也可以在设计set的数据类型时设计为结构体,其中放一个最新的时间参量),以此来更新时间参量。如果我们要替换的line的valid为1,则发生了一次eviction。
partA完整代码下载
运行结果:
转置矩阵
最简单的转置实现:
1.最多只能定义12个局部变量。
2.不允许使用位运算,不允许使用数组或者malloc。
3.不能改变原数组A,但是可以修改转置数组B。
1.block的大小为32byte,即可以放下8个int,即miss的最低限度是1/8。
2.cache的大小为32*32,即32个block,128个int。
3.blocking是一种很好的优化技术,这次实验基本就靠他了;)其大致概念为以数据块的形式读取数据,完全利用后丢弃,然后读取下一个,这样防止block利用的不全面。可以参考卡耐基梅隆的一篇文章:waside-blocking
4.尽量将一个block读入完全或者写入完全,例如假设一个block可以放两个数,进行如下转置操作,其读取时“尽力”读取,完全利用了一个block,但是在写入的时候浪费了1/2的空间。
5.尽量使用刚刚使用的block(还是“热乎的”),因为它们很可能还没有被替换,hit的概率会很大。
6.读出和写入的时候注意判断这两个位置映射在cache中的位置是否相同,(我们这个cache是直接映射,一个set只有一个block,所以绝大部分的miss伴随着替换),也可以说,我们要尽量避免替换的发生。
下面我结合实验要求的三个例子具体讲。
32 × 32 (M = 32, N = 32)
由于我们的block能存8个int,所以blocking的数据块最好是以它为单位的,这样能尽可能利用block,例如8 * 8或者16 * 16。
在32*32的情况中,一行是32个int,也就是4个block,所以cache可以存8行,由此可以推出映射冲突的情况:只要两个int之间相差8行的整数倍,那么读取这两个元素所在的block就会发生替换,再读后面连续的元素也会不断发生抖动(thrashing)下图中标出了与一个元素冲突的位置(包括他自己本身的位置,因为我们A,B两个数组在内存中是相邻的,而32*32又是cache的整数倍。):
但是转置的过程中这样的情况会发生吗?图中的BCD三点对于A来说仅仅是行差了8K,这在转置中是不可能发生的!因为转置是将A[i][j]送到B[j][i],不会有B[i][j+8k]的情况出现。
但是对于A点而言,如果A[i][j]中i = j,那么B也会是B[i][j],即映射遇到同一个block中,而当i = j的时候,就是对角线的情况:
所以现在我们只要单独处理对角线的情况就可以啦,这里有两种处理方法:
由于我们可以使用12个局部变量,所以我们可以用8个局部变量一次性将包含对角线int的block全部读出,这样即使写入的时候替换了之前的block也不要紧,因为我们已经全部读出了。
我们用一个局部变量暂时先保存这个对角线元素,并用另一个变量记录它的位置,待block的其他7个元素写完以后,我们再将这个会引起替换的元素写到目的地。
下面的代码使用第一种方法,另外,由于相差8行就会有冲突,所以我们blocking的时候用8*8的数据块。
64 × 64 (M = 64, N = 64)
此时,数组一行有64个int,即8个block,所以每四行就会填满一个cache,即两个元素相差四行就会发生冲突。
如果我们使用4*4的blocking,这样固然可以成功,但是每次都会有1/2的损失,优化不够。如果使用刚刚的8*8的blocking,那么在写入的时候就会发生冲突:
这个时候可以使用一下“divide and conquer”的思想,我们先将8*8的块分成四部分:
本来我们是要将右上角的2移动到左下角的3的(转置),但是为了防止冲突我们先把他们移动到2的位置,以后再来处理:
对于3和4,我们采取一样的策略,就可以得到如下结果,在这个过程中没有抖动的发生:
这个时候再将23互换就可以啦。
但是,测试以后并不能满足优化的要求,说明我们将23转换的时候(或是之后)又发生很多miss,所以我们应该在将右上角的34转换的过程中将2的位置复原,这里的复原是整个实验中最具技巧性的,由前面的要点5:尽量使用刚刚使用的block(还是“热乎的”),因为它们很可能还没有被替换,hit的概率会很大。我们在转换2的时候逆序转换:
同时在读取右上角34的时候按列来读,这样的好处就是把2换到3的过程中是从下到上按行换的,因为这样可以先使用“最热乎”的block:
接着转换:
最后的效果:
61 × 67 (M = 61, N = 67)
这个题只要求miss < 2000,比较宽松。
这个时候由于不对称,所以也不存在相差4行就必定冲突的情况,我们可以试一下16 * 16这种blocking。但是“对角线”的元素(横坐标等于纵坐标)肯定还是会冲突的(其实这个时候不是对角线了,因为不是正方形)。我们在这里用32*32分析中的第二种方法。
partB完整代码下载
最终结果为满分: