本節書摘來自華章社群《c語言程式設計:問題與求解方法》一書中的第3章,第3.10節提高部分,作者:何 勤,更多章節内容可以通路雲栖社群“華章社群”公衆号檢視
3.10 提高部分
在計算機的内部所有數和碼都是二進制的,我們必須對其有所了解,在程式設計中遇到困難或障礙時才不至于束手無策。
計算機内部的二進制數的表示多數與手寫表示的二進制數有所不同。
3.10.1 機内形式的整數
(1)無符号整數
無符号整數即非負整數,與手寫表示法相同。
在計算機中,無符号整數可用1個、2個、4個或8個位元組來存儲和傳輸。
1個位元組的位串能夠表示的數值範圍是0~255(即11111111=28–1)。
2個位元組的位串能夠表示的數值範圍是0~65535(即216–1)。
4個位元組的位串能夠表示的數值範圍是0~4294967295(即232–1)。
但讀者要注意:在程式設計時,盡量統一采用有符号數(變量與常量),在可以不使用無符号數的情況下,盡量不要用無符号數,以避免類型轉換帶來的很多麻煩。
(2)有符号整數
有符号整數又稱為“真值”。因為真值有正負号,是以在計算機中無法直接用位串來表示真值,要采用某種編碼來間接表示有符号整數。
在某個取值範圍中的所有有符号整數構成了一個(有限個元素的)集合。是以,當然可以用一定長度的二進制位串來對其進行編碼 。用二進制位串通過編碼來表示有符号整數時,有多種編碼規則,最常用的有原碼、反碼和補碼。
原碼表示法
“原碼表示法” 編碼規則規定:用位串最左邊的一位(通常稱為最高位)表示該數的符号位:0表示正數,1表示負數,其餘各位表示該數的絕對值。下表是一些用1個位元組表示的典型數值的8位原碼。
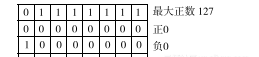
可見,将原碼表示的二進制有符号整數轉換成十進制整數很簡單,隻要将最高位轉變成正、負号,将剩下的其餘各位用前面學過的方法轉變成十進制整數即可。比如,10011011就是十進制數–27。 值得注意的是,原碼表示法中有兩個0值:正0和負0。
補碼表示法
但是,在計算機的設計制造中,人們卻偏愛采用補碼(編碼規則)來間接表示有符号整數。
對于在–128~127之間的真值,人們可以做兩個數的加法,隻要對兩個絕對值一樣而符号相反的數做加法,結果就是0。我們如何設計位串長度為8位的“補碼”來做類似的事呢?
位串長度為8位的補碼是這麼設計的,正數的補碼值就是所對應的無符号整數;而一個負數的補碼值是這樣得出來的:要求該補碼值在與其絕對值一樣大的無符号整數做加法時,結果應當是100000000(注意:一共有8個0)。
也就是說,隻要将向更高位的進位直接舍棄,補碼也遵守同樣的準則:兩個絕對值一樣而符号相反的補碼做加法,其結果是0。
由此,我們很容易得到求一個真值為負數的(位串長度為8位的)補碼的方法:先求出它所對應的二進制正數a,然後将其每一位都取反得到另一個二進制數b(即将a中的0變成1,1變成0)。這樣的兩個二進制數相加(a+b),必然等于11111111(8個1),最後将b再加上1,這樣就得到了一個負數的補碼,此數與其等值的正數的補碼相加,一定會等于100000000。
舉例來說,求真值–25的補碼,先求25的補碼得到00011001,然後每一位都取反得到11100110,然後再加1得到11100111,這就是真值–25的補碼。
由于位串長度為8位的補碼表太長,我們來研究位串長度為4位的補碼,見下表。
注意:從上表可看出,正數補碼的最高位都是0,而負數補碼的最高位都是1。
取表中有代表性的幾個資料進行相加,看看它們的真值運算和補碼運算有何對應關系。
1)大正數加小負數。
用真值運算:6+(–3)=3
用補碼進行運算: 0110+1101=10011,舍棄4位外的最高位,得到用補碼運算的結果0011,這恰好也是二進制形式表示的3。
2)小正數加大負數。
用真值運算:2+(–7)=–5
用補碼進行運算:0010+1001=1011,得到用補碼運算的結果是1011,查表可看到,補碼1011所對應的真值恰好也是–5。
3)負數加負數。
用真值運算:(–1)+(–7)=–8
用補碼進行運算:1111+1001=11000 ,舍棄4位以外的最高位,得到用補碼運算的結果是1000,查表可看到,補碼1000所對應的真值恰好也是–8。
延伸與拓展: 如何從補碼的運算結果中求得十進制的真值?
如果最高位為0,隻要将此正整數轉化十進制整數即可;如果補碼結果的最高位是1,說明該結果是一個負數,那麼與該負數的補碼所對應的二進制的絕對值該如何求得呢?答案很簡單:對運算結果每一位取反後再加1(這還是因為:若将該負數的補碼與其絕對值一樣大的正數做加法,其結果仍然應當是100000000)。
結論:對負數的補碼再次求補(即将每一位取反後再加1),得到的是該補碼所表示的數的(二進制形式的)絕對值。
例如,假設補碼運算的結果是1011,如何求得它所對應的絕對值的大小呢?因為它的最高位為1,表明結果是負數。對其再次求補碼(每一位取反後再加1),即可得到該補碼所表示的數的絕對值為(0101)2=5。是以,補碼運算結果用十進制真值來表示就是–5。
補碼運算中的溢出
在一定長度的補碼系統中,兩正數的補碼(最高位同為0)之和或者兩負數的補碼(最高位同為1)之和可能會超出該補碼系統所能夠表示的最大、最小數。如何判斷運算結果是否溢出呢?隻要看運算結果的最高位是否變了号(這是充分必要條件)。例如,真值運算(–7)+(–5)=–12,但是經查表得到用4位補碼進行的運算結果卻是:1001+1011=(1)0100,等于4,符号位從1變成了0 ! 這就産生了溢出。
符号位的擴充
一個補碼表示的有符号數在進行擴充時,直接用它的符号位複制到高位位元組中(即提升到位元組數更多的有符号整型時),這稱為“符号位擴充”。
計算機硬體為何要用補碼進行算術運算
為何計算機要如此麻煩地使用補碼來進行算術運算,而不使用人們更容易懂得的原碼來進行運算?
簡單地說,這是由于用原碼運算會出現麻煩—符号位在某些情況下不能直接參與運算,比如(10000001)原+(00000001)原=(10000010)原=(–2)10,這明顯不對。而且原碼還出現了兩個0(正0:00000000和負0:10000000)的問題。
而采用補碼來進行運算,以上這些問題都迎刃而解!符号位與數字位可以一并參與算術運算,如果有向更高位的進位(即在最高符号位上産生了向高位的進位),隻要直接把它舍棄即可。采用補碼後,所有減法都可用加法代替,節省了制造算術邏輯單元的成本(不必制造實作減法的電路,在算術邏輯單元中隻要有“全加器”電路即可)。
(3)計算機中使用補碼的流程
計算機中使用補碼的過程如下:
程式設計(或在程式運作時輸入)的有符号整數(即十進制的真值)
數值被編譯程式(或由輸入庫函數)轉換成補碼
硬體(alu)用該數補碼進行算術運算(代替用真值進行運算)
由輸出庫函數将結果轉換成十進制的真值輸出
操作者最終看到十進制的結果
由此可見,對于一般的程式設計者來說,隻要程式運作不會出現溢出問題,不需修改程式将補碼進行符号位的擴充,不需要使用補碼表示的資料拆開來進行位運算,在編寫源程式中,通常不必考慮有符号整數在機内是用補碼來表示的這個底層問題。
(4)類型提升時的符号位擴充
補碼表示的有符号整數在進行類型提升時,即由短位串變為長位串時(比如,由int型提升為long int型),隻要将符号位進行擴充即可。
比如,一個位元組的補碼表示的有符号數01101000(正數)和11010110(負數),提升為兩個位元組的補碼表示的有符号數分别就是:0000000001101000 (正數)和1111111111010110(負數),低8位沒有發生任何變化,隻需将符号位向高位擴充即可:符号位是0,擴充的高位位元組就全部填充0,符号位是1,擴充的高位位元組就全部填充1。隻有這樣,才能確定在類型提升後的補碼所對應的真值與提升前的原來真值一樣大。
然而,一個無符号的整數在類型提升時采用的規則,卻是将擴充的高位位元組全部填充0。
提示:正是由于無符号整數類型提升時(高位都填充0)與用補碼表示的有符号數的類型提升有着根本不同,是以,本書不提倡将無符号數和有符号數混用在同一個表達式中,以免類型轉換時出現麻煩。萬一不得已必須放在一個表達式中,在類型轉換時要特别小心,避免犯錯誤。
3.10.2 二進制浮點數在計算機中的表示方法
不通過某種編碼,計算機中無法直接存儲手寫的小數形式的實數–110110.101或規範化的指數形式的實數–1.10110101×2101。小數點前面隻有一位非0的整數,就是規範化的指數形式表示的實數;在二進制中,小數點左邊的這個非零整數隻能是1。
在計算機中,對實數的編碼(比如以下所講的餘127碼)是以對二進制的規範化的指數形式為基礎來進行的。其編碼方式是:省略掉規範化的指數形式中的一位整數部分“1”、小數點“.”、乘号“×”、基數2,隻保留數的符号(用0表示正數、1表示負數)、尾數(即實數的小數部分)和指數部分。這就必須規定在位串中這三者的位置和各自所占的位元組數。
比如,對于–1.10110101×2101這個數,隻需存儲符号位(負号)、尾數位10110101和指數位101。
此外,指數部分還要變換。因為在計算機中,ieee(電氣和電子工程師協會)745标準規定:用長度為8位的餘127碼(而不是用補碼)來表示(可正可負的)指數部分。
在計算機中通正常定:從左到右采用“符号位(1位)+指數位(8位的‘移碼’或稱為餘127碼)+尾數位(23位)”的方式(一共占據4個位元組)來表示和存儲一個二進制的單精度實數(又稱為單精度浮點數)。
這是由ieee 745标準規定的一種二進制實型數表示法,精度是十進制的6位(見behrouz forouzan等著,劉藝等譯《計算機科學導論》,機械工業出版社出版)。大多數計算機制造商都支援這種ieee 745标準。
【例題3.4】求一個十進制數–41.75的餘127碼的實數表示法。
1)符号為負,是以最左邊符号位s=1(如果是正數,符号位用0表示)。
2)十進制轉換為二進制 41.75=(110011.11)2。其中,整數和小數部分分别轉換。
3)規範化:(110011.11)2=(1.1001111×2201)(即移動小數點)。
4)指數位的餘127碼為 e=101+1111111=(10000100)2(即5+127=132)。
5)尾數位為 m=(1001111)2。
6)最終得到:
對于負數情況完全是類似的,絕對值最大的負數是–3.4×1038,絕對值最小的負數是–1.17×10–38。
單精度浮點數的精度
浮點數的精度取決于它的規範化表示法的尾數部分,與指數位無關。指數位僅決定小數點的位置。尾數部分的位數越多,能夠表示的有效數字就越多,精度就越高。
在ieee 745标準中,單精度浮點數的尾數用23位存儲,加上預設的小數點前的1個整數位(該位的值是1)。用24位二進制能夠表示的最大十進制正整數是224–1=16777215,是以單精度的浮點型數的精度是十進制的7位。也就是說,隻有十進制數值的高7位是準确無誤的(嚴格來說,如果一個十進制數的高8位小于等于16777215,那麼這個數的高8位都是準确無誤的,否則精度隻有7位)。
實數值0.0規定用餘127碼的全0來表示
用以上轉換方法,規範化指數表示法的0無法用餘127碼來表示,因為它沒有一位非零的整數部分。是以,ieee 745标準特别規定:用餘127碼的全0來表示數值0,即0 00000000 000000000000000000000。