本節書摘來自華章計算機《資料科學r語言實踐:面向計算推理與問題求解的案例研究法》一書中的第2章,第2.6節,作者:[美] 德博拉·諾蘭(deborah nolan) 鄧肯·坦普·朗(duncan temple lang) 更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
櫻花公路賽的結果包含20~80歲的運動員的比賽記錄。然而,不會有任何一個運動員的記錄滿足60年的跨度。由于我們隻有14年的比賽記錄,是以最多隻能觀察到一個運動員20~33歲的記錄,或者一個80歲的運動員從他67歲之後的記錄。是以,滿足60年的跨度是不可能的。這意味着,當研究随時間推移的個人成績時,我們看到的是長度最多有14年的短時間序列。研究20~80歲的成績意味着我們必須依賴資料的橫截面資訊,而這樣的資訊需要在這些短的時間序列裡獲得。
可以合理地猜測在一個短的時期内,比如8~10年,一名選手的成績大緻與年齡成線性關系(我們已經從橫截面資料的分段線性模型中得到了這樣的結論)。我們可以繪制圖形以确定是否屬于這種情況。現在有300多名參賽選手的資料可以用來繪圖,為了限制過度繪制的影響,我們針對不同資料子集繪制多張圖形。首先我們将參賽選手分成9組,在3×3的網格上繪制9張圖,配置設定給每組大緻相同數量的選手:
為每一幅圖建立一個空白畫布。例如,
然後我們在組内為每個選手添加線段,使用不同顔色和類型的線段以區分不同的參賽選手。下面的addrunners()函數為每個選手添加一條線段:
我們可以建立9塊空白的畫布,并用以下代碼為參賽選手添加線段:
invisible()函數隐藏了sapply()函數的傳回值。由于該函數的功能是将線段添加到畫布上,是以對于每次疊代它都傳回null,可以安全地忽略該傳回值。
在圖2-17中,可以看到9幅曲線圖,每幅圖大約包含30名運動員。有些運動員的成績波動有點大,我們可能需要重新回顧一下舍棄參賽選手的概念,即由于選手的成績波動超出了預期,是以有可能是兩個不同運動員記錄的合并,需要将他們舍棄掉。這裡我們将以上處理留作練習。另外,為每位選手的成績拟合一條直線似乎更合理。
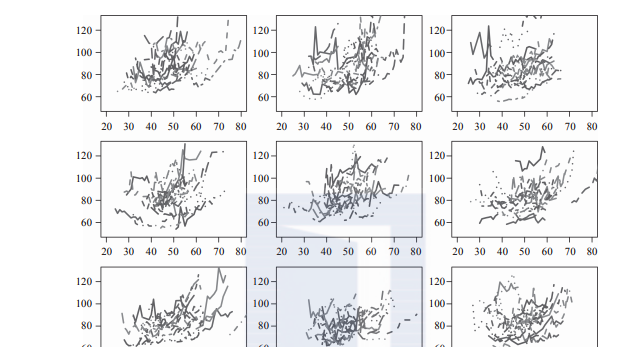
圖2-17 多場賽事的比賽用時。這些曲線圖表示至少完成8次櫻花賽的男選手的跑步時間。每個連接配接的片段集合對應一位運動員的跑步時間。觀察所有的曲線圖可以看出,該圖和圖2-7中的散點圖呈現相似的形狀,例如,圖形随着年齡向上彎曲。然而,我們也可以看到單個選手成績的變化情況。例如,許多中年選手的跑步時間随着年齡的增長而迅速增加,但并不是所有人都這樣。他們中的一些人的成績在進步,而另一些人的成績變化較慢
針對個體選手的縱向分析隐式地抑制了那些可能影響成績的協變量,比如性别。其中一個例外就是任意給定年份的比賽條件—由于路線或天氣的變化,一些年份的速度可能慢些,一些年份速度可能快些。然而,看似合理的是這樣的影響跟年齡無關,是以它相當于測量噪聲。
現在有了參賽選手的名單,我們希望将每位選手的成績拟合成一條線。如果針對一位選手編寫函數執行該處理,那麼就可以把該函數應用到名單上所有的選手。這個函數需要怎麼做呢?可以讓它通過lm()函數拟合一條線。函數需要傳回什麼值呢?我們對傳回年齡的系數感興趣,但是需要能夠在年齡的上下文中對它進行解釋。由于有每位選手的多個年齡,那麼就讓我們傳回一個年齡的中間值。并且在得到該值後,傳回一個該年齡上選手成績的預測值。需要為函數輸入什麼呢?實際上僅僅是參賽選手的比賽用時和年齡。我們可以将它們作為獨立的參數傳入函數或者傳入我們的資料框中。如果是後者,我們需要知道要拟合的變量名。下面完成這項工作。我們還讓函數将被拟合的線段添加到繪圖中。也可以通過增加參數使其變為可選操作,該參數的預設值為false,僅當指定參數為true時函數才添加線段。該函數如下:
這裡我們留一道練習題,增強以上函數的功能,使它也可以傳回年齡誤差的sd(标準差)以及年齡系數的se(标準誤差)。另外,我們也将另一種可選方法留作練習,即同時拟合所有運動員的線段,使噪聲分散在所有運動員上。
針對圖2-17中的一幅曲線圖,我們可以用fitone()函數添加拟合曲線,代碼如下:
觀察圖2-18中的黑色虛線,這些線段似乎捕捉到了每個運動員的成績變化。
圖2-18 單個選手的跑步時間關于年齡的線性拟合。這裡我們用最小二乘法對每個運動員的比賽用時進行拟合,以增強圖2-17右下角的曲線圖。總共有30條左右單個選手的黑色虛線段
接下來檢查運動員與運動員之間的差異,我們使用以下調用對全部306位運動員進行線性拟合:
現在,對至少參賽8次的運動員(且在這些參賽年度中所居住的州名相同),我們用一個單一系數表示比賽用時和年齡之間的關系。這個系數以分鐘為機關,也是每年10英裡賽比賽的時間機關。如果系數為正,表示該參賽者因速度變慢而使每年比賽用時增加的分鐘數。
從圖2-19可以發現這些系數是如何随年齡進行變化的。大量參賽選手的個人成績發生了變化,很多人在30歲以後開始變慢,而少量的人在他們50多和60多歲期間跑得更快。不管怎樣,我們還是可以看到年齡和比賽用時之間的關系,在系數方面呈線性正相關趨勢。可以用如下方式進行拟合:
拟合的概要資訊如下:
圖2-19 運動員的縱向分析系數。該散點圖顯示了對300多位參賽選手進行直線拟合的斜率,這些選手都至少完成了8次櫻花賽。系數為負表示參賽選手随着年齡增長速度變得更快。該圖包括一條基于最小二乘法的拟合直線和一條loess拟合曲線。注意幾乎所有超過50歲的選手的系數都為正值。對于50歲的選手,系數的典型值是每年大約1分鐘
在圖中我們沿着0水準參考線添加拟合直線,同時使用loess()函數畫出平滑系數拟合曲線。該圖表明,在平均情況下,年齡低于35歲的運動員的成績有所提高。也就是說,低于35歲的選手的年齡系數是負值。假設的“平均”參賽選手在年齡超過35歲以後跑步開始放慢。到60歲時,這個典型選手每年大約會慢1.3分鐘,大緻是橫截面分析法顯示結果的2倍。