本節書摘來自華章計算機《算法基礎》一書中的第2章,第2.3節,作者:(美)羅德·斯蒂芬斯(rod stephens)著,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
有時程式需要計算某數的正整數次幂,這在該幂指數不大時容易完成。例如,73可以通過計算7×7×7很容易地得到結果343。對于較大的幂,例如7102×187×291,這種計算過程是十分緩慢的。
注 計算較大的幂如7102×187×291可能很緩慢。但如果不是這種求幂運算在某些重要密碼學中得到應用,人們也許不會十分關心它。
幸運的是,有一種較快的方法來執行這種運算。這種方法基于乘方運算的兩個關鍵法則:
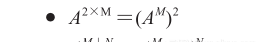
當這個幂是二次幂時,第一個法則可以迅速地計算出a的幂。
第二個法則能将這些a的幂結合以産生想要的結果。
以下僞代碼展示了這個算法:
例如要計算出76。首先算法計算出71、72、74。由于下一個指數8比所需的6大,是以算法停止。
接下來算法使用第二個法則來從已經産生的二次幂中生成76。如果将6看作2的幂的和,6=2+4。使用第二個法則,得到76=72×74=49×2 401=117 649。
執行這個運算進行兩次乘法來計算72和74再加上一次乘法來獲得最終結果,即總共進行三次乘法運算。這比簡單計算7×7×7×7×7×7進行了更少的乘法運算,但在本例中這隻是一個小小的不同。
更普遍地,對于指數p,算法進行log(p)次運算來得到a的p次幂。然後算法檢驗a的二進制位數來确定它應當将其中的哪些乘在一起以獲得最終結果。(如果p的二進制位數是1,那麼最終的結果應當包含2的相應幂。在前例中,6的二進制表示是110,是以需要計算2的二次幂和四次幂,即22和24。)
在二進制中,數值p有log2(p)位,是以總共的運作時間複雜度是o(log p)+o(log p)=o(log p)。即使p為一百萬,log(p)大約隻有20,是以這個算法需運作20步左右(至多40次乘法)。這比一百萬要小得多。
這種算法的一個限制是當指數很大時,幂增長得過快。即使一個如7300這樣“小”的值也有254個十進制位。這意味着用來計算大指數幂龐大數相乘的過程是緩慢的,并且需要大量計算空間。
幸運的是,這種龐大的幂運算的最常見應用是加密算法,這種算法的運算限制在某個模中。盡管這個模通常較大,但仍能限制住運算數和結果的大小。例如如果某模有100位,兩個100位數的積就不會大于200位。那麼,接下來可以再次用這個模來得到一個不大于100位的結果。雖然用模将每一個數減小使得每步運算稍微變慢,但也意味着可以計算幾乎無限大的值。