本節書摘來自華章出版社《短文本資料了解(1)》一書中的第2章,第2.3節,作者王仲遠,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
本節首先直覺地讨論屬性的打分原則,進而介紹如何處理cb和ib清單以完成對屬性的打分,最後讨論如何聚合不同資料源的屬性得分。
這項工作的目的在于計算屬性概念對的p(a|c)數值。這個機率分數對機器推測有很大作用。
這個機率分數被定義為典型度(typicality)。在認知學和心理學上[104],典型度被用來研究為什麼某些實體因為某個概念而被人類特别提起。例如,dog為pet的典型實體,因為它被頻繁地當成pet提及,而且它與其他的pet實體具有很高的外形相似度[164]。同理,上述直覺可被用來研究屬性的典型度。
如果屬性a為概念c的典型屬性,它應滿足兩個原則:
a與c常常共同出現(頻率)。
a在c的實體的屬性中很常見(家族相似度)。
根據上述直覺,population是country的一個典型屬性,因為二者在cb和ib清單中被頻繁觀測。更進一步,這是由于大多數country的實體,比如china和germany,都有population這個屬性。
上述論證證明了使用cb和ib量化p(a|c)的意義。二者都考慮了頻率原則并且ib還考慮了家族相似度原則。相比之下,大多現有工作沒有考慮這兩項原則或隻考慮了其中一項,如,參考文獻[126,82,124,160]隻考慮了頻率;參考文獻[125]隻考慮了家族相似度;參考文獻[122,138]沒有考慮任何原則,而是使用屬性的語境相似度。
下面将講述如何從cb清單中将頻率實體化,以及如何從ib清單中将頻率和家族相似度實體化。
回顧一下,cb清單的格式為(c,a,n(c,a))。按概念c為清單分組,可得到概念c的一系列屬性a,以及它們的頻率分布。給出這些資訊,典型度得分p(a|c)可被計算為:
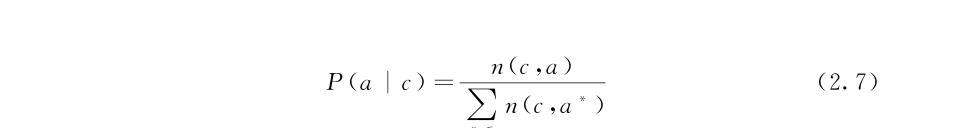
下面闡述根據ib清單(i,a,n(i,a))計算典型度的方法。如前文所述,三組ib清單分别從網頁文本、搜尋日志和知識庫中擷取。這三組清單的品質在不同的概念c上有差異。因而,本章方法分别計算三組清單的典型度得分,然後将三組得分同cb清單的得分聚合。
為将ib模式聯系到概念上,p(a|c)被展開為:
基于這項展開式,任務被轉化為計算p(a|i,c)和p(i|c)。舉例而言,考慮ib模式“the age of george washington”,如果機器知道“george washington”是概念president的實體,那麼這句話可以被用來計算屬性age和概念president之間的典型度得分。在上式中,p(a|i,c)可将age和president間的典型度量化,而p(i|c)表示實體“george washington”對概念president的代表性。
通過probase計算p(a|i,c)和p(i|c):p(a|i,c)和p(i|c)可以基于probase計算。probase記錄着“george washington”對概念president的代表性。為友善表達,下面假設一個實體隻屬于一個概念,後文将讨論去除該假設的情況。
首先計算p(a|i,c)。在p(a|i,c)=p(a|i)的假設下,p(a|i,c)可被計算為:
是以,這一任務被轉化為從probase擷取p(c|i)。在先前的簡化假設下,p(c|i)表示概念c對某一實體i的代表性。在probase中如果這對概念和實體被觀測到,則p(c|i)=1,否則p(c|i)=0。
在實際情況中,一個實體可能屬于多個概念,進而衍生出如下兩種情況:
[c1]有歧義的實體與不同的概念相關:“washington”可能表示president或state,而這兩個概念的典型屬性很不相同。簡單的計算方式會導緻将population錯誤地鑒别為概念president的典型屬性。
[c2]無歧義的實體與相同的概念相關:即使某一實體沒有歧義,它也有可能出現在不同的語境中。例如,“george washington”可能代表一個總統(president)、愛國者(patriot)或曆史人物(historical figure)。屬于不同概念的有歧義實體計算出的p(i|c)理論上應比屬于相似概念的無歧義實體計算出的值低。簡單的計算不能考慮概念間的相似性。
基于上述分析,我們的任務是無偏見地估算p(a|i,c)和p(c|i)的值。
p(a|i,c)和p(c|i)無偏見化:下面介紹如何無偏見化p(a|i,c)和p(c|i),以解決c1和c2兩種情況。
首先計算p(a|i,c),如果實體i有歧義,一個從别的概念中擷取的更高n(i,a)值不應被考慮。例如,雖然population與washington常常共現,在state name語境下,population不應被考慮成president的屬性。是以,相交率(join ratio,jr)這個概念被使用來表示屬性a與概念c相關的可能性。
其中jc(a,c)被定義為概念c中的實體含有屬性a的次數,這将a的家族相似度量化。通過觀察,population之于president的jr得分接近0。這是由于概念president中的大多實體,如“george bush”,都沒有population這個屬性。
基于這個觀念,式(29)可被去偏見化:
其中n(i,a,c)=n(i,a)jr(a,c)。
接下來計算p(c|i)。考慮一個實體屬于多個概念的情況,如c2,p(c|i)可通過probase中的頻率統計np(c,i)計算:
然而,使用上述公式不能很好地區分c1和c2。因而,我們通過計算兩個概念c和c*之間的相似性來降低那些從不相似概念中擷取的頻率的權重。這一相似性可通過probase,使用兩個實體集的jaccard相似分數來計算。通過這一取值為0~1的相似分數sim(c,c′),p(c|i)可被計算為:
其中nu(c,i)=∑c′np(c′,i)sim(c,c′)。這樣一來,不僅歧義問題得以處理,頻率和家族相似度兩項典型度原則也得以反映。
表24對比了式(213)和式(214)得出的p(i|c)。去偏見化前,有歧義實體的p(i|c)被過高估計,比如“washington”。去偏見化後,其數值明顯降低。相比之下,實體“bush”雖與兩個總統相關,但都對應president這個概念,因而應在president這個概念上得到較高得分。通過觀察,去偏見化的結果符合這一原則,比如說“george washington”和“bush”的p(i|c)分數都比“washington”的要高。
表25描述了去偏見化是如何改進president這個概念的屬性典型度排名的。表中所列的不屬于president的屬性在排名上都有不同程度的降低。這是由于在去偏見化前,“washington”的p(i|c)被高估,但其還可能屬于state這個概念,這會導緻與state相關的屬性在president上也獲得較高得分。
本節前面部分讨論了如何從cb網頁文本清單中計算p(a|c),以及如何從ib的三個清單(網頁文本、搜尋日志和知識庫)中計算該值。我們将這四個得分分别标記為pcb(a|c)、pib(a|c)、pqb(a|c)和pkb(a|c)。
要聚合這些得分并不是一項簡單的工作,不同的分數來源對不同的概念有着互補的優勢。對于包含很多有歧義的實體的概念,ib擷取的得分置信度較低。比如,概念wine中的很多實體具有歧義,像“bordeaux”和“champagne”可以表示city的名字,進而具有city相關的屬性,如mayor。在此例中,ib擷取的得分置信度較低。然而在其他情況下,當概念可被擴充為大量無歧義的實體時,ib給出的得分則十分可靠。
這些觀察表明單資料源不可能為所有概念給出可靠的得分,因而應将不同來源的得分聚合。我們希望算法能夠基于概念特征自動為得分調整權重,進而為所有的概念給出可靠的得分。同現有的方法不同,這一新的算法架構可被應用于大量概念之上。
更為正式地,p(a|c)的計算可被轉化為:
目标被轉化為學習某一概念的相關權重。
這項任務采用線性核函數的ranking svm方法。該方法為一種常見的pairwise排序算法,同回歸算法相比,其優勢在于訓練資料不需要具備準确的典型度得分标簽。這符合問題的需求:雖然不能得到某一屬性(比如population)的絕對得分,但可以陳述population比picture更典型這一事實。通過收集這樣的成對比較資料作為訓練資料,式(215)中的權重可被訓練得到。
更為正式地闡述,來源m的權重wm為fim的線性組合,其中特征為實體i的歧義度或模式的統計顯著性。
f1m(avg mod bridging score:bridging score[121]通過實體是否屬于不同概念來度量它的歧義度。
直覺上說,這一分數在包含歧義的實體上較低,如“washington”。實驗表明,bridging score的一種變換mod bridging score更為有效。
f2m(avgp(c|i)):當實體屬于很多不同的概念時,p(c|i)的值較低,因而它也可以作為實體歧義度的度量。
f3m(∑(frequencym(a))/#attributem):當平均每屬性的屬性頻率較低時,統計顯著性較低。
f4m(∑(frequencym(a))/#instancep):當平均每實體的屬性頻率較低時,統計顯著性較低。
f5m(#attributem/#instancep):當概念中實體的平均屬性數較低時,對該概念的特征提取有效性較低。
更為正式地,wm可被表示為五個特征的線性合并wm=w0m+∑kwkmfkm。式(215)可被擴充為下式。
可見,這是一系列元素的線性變換。線性核函數的ranking svm算法可被用來學習參數。同已有的方法不同,上面提出的方法不需要覆寫所有概念的訓練資料。
将概念和屬性的關系量化後,我們得到一系列概念的屬性。由于這些屬性從網站擷取,人們可能會使用不同的詞來表示相同的含義,比如mission和goal都表示目的。
因而,另一項重要工作為将同義屬性分組。若不進行這項工作,相同意義的屬性會被分散稀釋。
本章方法借助wikipedia[100]找尋同義屬性,具體采用如下方式:
wikipedia重定向:一些wikipedia連結沒有自己的頁面,通路這些連結會被重定向到相同主題的其他文章。下文使用xi→yi表示重定向。
wikipedia内部連結:wikepedia的内部連結被表示為[[title|surface name]]。其中surface name為目前文本,title為連結到的網頁。下文同樣用xi→yi表示連結關系。
使用這些關系對可以連結同義屬性。所有相連的屬性可被視作一個屬性聚類。在一個聚類内,頻率最高的屬性被當作該屬性聚類的代表屬性。