本節書摘來自華章計算機《編寫高品質代碼:改善c程式代碼的125個建議》一書中的第1章,建議3-4,作者:馬 偉 更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
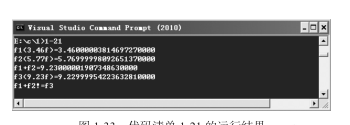
在整型資料中,我們一般都使用“==”操作符來判斷兩個數是否相等。在浮點資料的運算中,也存在着“==”操作符,那麼是否也可以使用這個“==”操作符來判斷兩個浮點數是否相等呢?帶着這個問題,示例程式如代碼清單1-21所示。
在代碼清單1-21中,分别定義了3個float變量 f1、f2與f3。從表面上看,f1+f2的值應該是9.23,是以執行條件判斷語句“if(f1+f2==f3)”時,應該傳回true。但實際的運作結果并非如此,如圖1-33所示。
要想使語句“if(f1+f2==f3)”傳回true,那麼f1+f2和f3在浮點格式的精度限制内必須嚴格相等。這也就意味着,一般情形下(0除外),浮點格式中的每一個位都必須相等。
由于浮點數存在誤差,即使是同一意義上的值,如果來源不同,那麼判斷也就可能不會為true。換句話說,在浮點計算中,“==”的作用是比較兩個浮點數是否具有完全相同的格式資料,而不是一般數學或工程意義上的相等。在浮點計算中兩個資料相等的含義通常是指在誤差範圍内,兩個資料的意義一緻(即二者描述的實體量的取值一緻,或者說相容),是以不能使用“==”操作符進行判斷。
既然不能使用“==”操作符進行判斷,那麼我們又應該怎樣正确判斷兩個浮點數是否相等呢?
一般情況下,浮點數的相等判斷通常使用如下形式,即:
示例代碼如下所示:
其中,epsilon是一個絕對的資料。采用這種形式來判斷相等,很顯然,如何确定Δ就成了問題的關鍵所在。Δ值的确定需要考慮數值背後的含義,而且它總是與誤差的概念相随。
(1)依據資料誤差進行判斷
如果兩個資料相差Δ,假設一個資料的誤差是Δ1,另一個資料的誤差是Δ2,那麼一個簡單的判據是:
https://yqfile.alicdn.com/0eededb373e73e53645f661c965e1b6292987982.png" >
實際上,如果資料不是直接來自某個測量裝置,而是某個仿真系統的輸出或者是測量資料經過一系列處理的結果,那麼Δ1和Δ2大多沒有确定的值。此外,這種方法在理論上也不夠嚴謹,隻是便于使用而已。
(2)依據允許誤差進行判斷
在許多情況下,計算精度和資料精度均遠遠超過了實際需求,使用資料誤差進行相等判斷除了加大計算量之外,沒有實際意義。此時,則可根據實際精度需求确定允許誤差,然後用允許誤差替代資料誤差進行相等判斷。這種方法更簡單,而且允許誤差一般遠大于資料誤差,可以減小計算量。不過,所謂的允許誤差往往沒有确定的值,主要依據經驗來判斷,是以有較大的不确定性。
雖然相對于“==”操作符,使用if(fabs(a-b) < epsilon)形式進行判斷是一個比較好的解決方案,但它卻存在着一定的局限性。比如,epsilon的取值為0.0001,而a和b的數值大小也在0.0001附近,那麼它顯然是不合适的。另外,對于a和b大小是10000這樣的資料,它也不合适,因為10000和10001也可以認為是相等的。
既然這種絕對誤差形式“if(fabs(a-b) < epsilon)”存在着局限性,那麼我們可以嘗試使用相對誤差的形式“fabs ( (a-b)/a ) < epsilon”進行判斷,示例代碼如下所示:
這樣的判斷形式看起來是可行的,但它同樣存在着局限性。因為它是拿固定的第一個參數做比較的,如果我們分别調用isequal(a, b, epsilon)和isequal(b, a, epsilon),那麼可能會得到不同的結果。與此同時,如果第一個參數是0,很可能會産生除0溢出。是以,我們可以把上面的判斷形式改造為:除數選取為a和b當中絕對數值較大的即可,示例代碼如下所示:
這樣看起來就更加完善了。當然,在某些特殊的情況下,相對誤差也不能代表全部。是以,我們還需要将相對誤差和絕對誤差結合使用。完整的比較示例代碼如下所示: