本節書摘來自異步社群《r語言初學指南》一書中的第1章,第1.6節,作者【美】brian dennis(布萊恩·丹尼斯),更多章節内容可以通路雲栖社群“異步社群”公衆号檢視
r語言初學指南
可用已學到的r知識來完成下面的計算題。最初可能會遇到些小麻煩,但通過實踐、試驗、犯錯并與同學讨論,就可掌握如何操作r。記住,如果輸入了錯誤的指令,隻要再輸入一遍正确的即可,r會覆寫之前的值。在指令運作成功并得到結果後,将其複制并儲存在一個文本檔案中,以便日後調用。
1-1 計算下列各表達式:
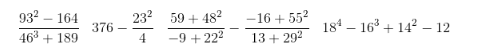
1-2 在更長的時間跨度下,再畫一遍投資方程圖(計算存單中的金額)。這次将時間延長到多年(50年?)後的将來,比如說一直到65歲退休那年。得到的圖形是不是很令人驚訝?這确實讓人很難抉擇:要麼現在去買一條設計新穎的牛仔褲,要麼把錢存起來,以後會獲得幾倍于其價格的存款。
再用幾種不同的利率計算一下,并将曲線添加到圖形中,看看能得到什麼不同的效果。
1-3 下表為美國整個曆史上的人口數量,資料來源于美國人口調查局。以時間為橫軸,以美國人口數量為縱軸,繪制線圖(type="l")。這裡提一下,可把人口資料四舍五入到10萬位,這對繪制的圖形幾乎不會産生影響。
用不同的繪圖類型重複做6次(type="p", type="b", type="c", type="o", type="h"及type="l"),并分别儲存每次的圖形。比較不同類型的圖形,找出各圖形分别可強調資料的哪些特征。
1-4 若在平地上以45°投出一個棒球,其初始速度為75mph(英裡每小時),則根據牛頓運動定律,t 秒之後,棒球水準位移x (不計空氣阻力)的表達式如下:
此外,若假設棒球的初始高度為5ft(英尺),則t 秒後,棒球距地面高度y 的表達式為:
在上面兩個方程中,已将距離x 和高度y 的機關換算為米。棒球将于4.09秒後落地。用r語言程式設計,時間t 的取值範圍為0到4.09秒,分别計算不同時間點上棒球的水準位移(記向量x )和高度(記向量y ),并以向量x 為橫軸,向量y 為縱軸繪圖。讀圖并根據圖中棒球的軌迹,确定棒球達到的最大高度及最遠距離的近似值。
注意:對不同的初速度及投擲角度,上述棒球方程中的系數值會不同。這些方程可寫成更一般的形式,以滿足不同的初始條件,但這将涉及部分三角函數的知識(第9章)。
1-5 根據牛頓萬有引力定律,由于太陽的引力,物體在太陽方向的加速度可由下式表示:
這裡r 表示物體到太陽中心的距離,計量機關為天文機關(astronomical units, au)。一個天文機關大約等于1.5億千米,這是地球到太陽的平均距離。為友善起見,在上面這種牛頓方程中,a 的機關設定為在一個天文距離(1 au)上物體所具有的加速度。利用該方程,計算各行星在距太陽的平均距離下的加速度分别是多少:
冥王星現被看作一個源于kuiper帶(kuiper belt)的大型類彗星物體或矮行星。
1-6 利用問題1-5中的方程繪圖,以r 值為橫軸,以加速度a 為縱軸。其中,r 取值從0.4個天文機關(水星的距離)到5.2個天文機關(木星的距離)。根據牛頓引力定律,是否存在某個距離,使物體可以完全脫離太陽的引力?
1-7 利用之前所學的狼-駝鹿系統中的捕殺率方程,進行一些數值上的研究或實驗,找出曲線從哪裡開始變得平穩(平均每隻狼的最大捕殺率)。怎麼才有可能有大于該最大值的實際資料?在方程中,是否有與平穩點相似的數值?
1-8 在農業中,為了減少殺蟲劑的使用,常用捕食性昆蟲來對付害蟲。其中,瓢蟲最愛捕食蚜蟲。桃蚜是一種對許多水果和蔬菜作物有嚴重危害的害蟲,在最近的一項研究中(pervez和omkar,2005),昆蟲學家們觀察到了用瓢蟲控制這種蚜蟲的可行性。在研究中,昆蟲學家們通過實驗驗證了三種不同瓢蟲對該蚜蟲的捕殺率:
将上表中每列資料作為輸入的向量,并用描述性名稱命名。以瓢蟲的捕食率和蚜蟲密度為坐标軸,用r對每種瓢蟲作散點圖(type="p")。然後,用下列數值作為方程中的常數,在圖中添加捕殺率曲線:
在繪制下一種瓢蟲圖形之前,别忘儲存并關閉前一幅圖。
1-9 再次用狼-駝鹿資料繪制散點圖,并用所有可行的圖形檔案格式(.jpg、.eps、.png、等)來儲存圖形。将各種格式的圖檔都輸入到文字處理軟體或示範文稿中,這樣就可兩兩比較不同格式的圖形。通過網絡研究來找出每種可行格式的主要優缺點,并在檔案中或示範文稿中,将每種格式的優缺點列舉在相應格式的圖形下面并分享你的結論!