<b>更多深度文章,請關注雲計算頻道:https://yq.aliyun.com/cloud</b>
<b>系列文章:</b>
<a href="https://yq.aliyun.com/articles/86580">一入侯門“深”似海,深度學習深幾許(深度學習入門系列之一)</a>
<a href="https://yq.aliyun.com/articles/88300">人工“碳”索意猶盡,智能“矽”來未可知(深度學習入門系列之二)</a>
<a href="https://yq.aliyun.com/articles/90565">神經網絡不勝語,m-p模型似可尋(深度學習入門系列之三)</a>
<a href="https://yq.aliyun.com/articles/91436">“機器學習”三重門,“中庸之道”趨若人(深度學習入門系列之四)</a>
原文再續,書接上回。
我們知道,《三字經》裡開篇第一句就是:“人之初,性本善”。那麼對于神經網絡來說,這句話就要改為:“網之初,感覺機”。感覺機(
perceptrons ),基本上來說,是一切神經網絡學習的起點。
很多有關神經網絡學習(包括深度學習)的教程,在提及感覺機時,都知道繞不過,但也僅僅一帶而過。學過程式設計的同學都知道,不論是哪門什麼語言,那個神一般存在的第一個程式——“hello world”,對初學者有多麼重要,可以說,它就是很多人“光榮與夢想”開始的地方。
而感覺機學習,就是神經網絡學習的“hello world”,是以對于初學者來說,也值得我們細細玩味。是以,下面我們就給予詳細講解。
在第3小節中,我們已經提到,所謂的感覺機,其實就是一個由兩層神經元構成的網絡結構,它在輸入層接收外界的輸入,通過激活函數(含門檻值)的變換,把信号傳送至輸出層,是以它也稱之為“門檻值邏輯單元(threshold logic unit)”。
麻雀雖小,五髒俱全。感覺機雖然簡單,但已初具神經網絡的必備要素。在前面我們也提到,所有“有監督”的學習,在某種程度上,都是分類(classification)學習算法。而感覺機就是有監督的學習,是以,它也是一種分類算法。下面我們就列舉一個區分“西瓜和香蕉”的經典案例,來看看感覺機是如何工作的[1]。
為了簡單起見,我們就假設西瓜和香蕉都僅有兩個特征(feature):形狀和顔色,其它特征暫不考慮。這兩個特征都是基于視覺刺激而得到的。
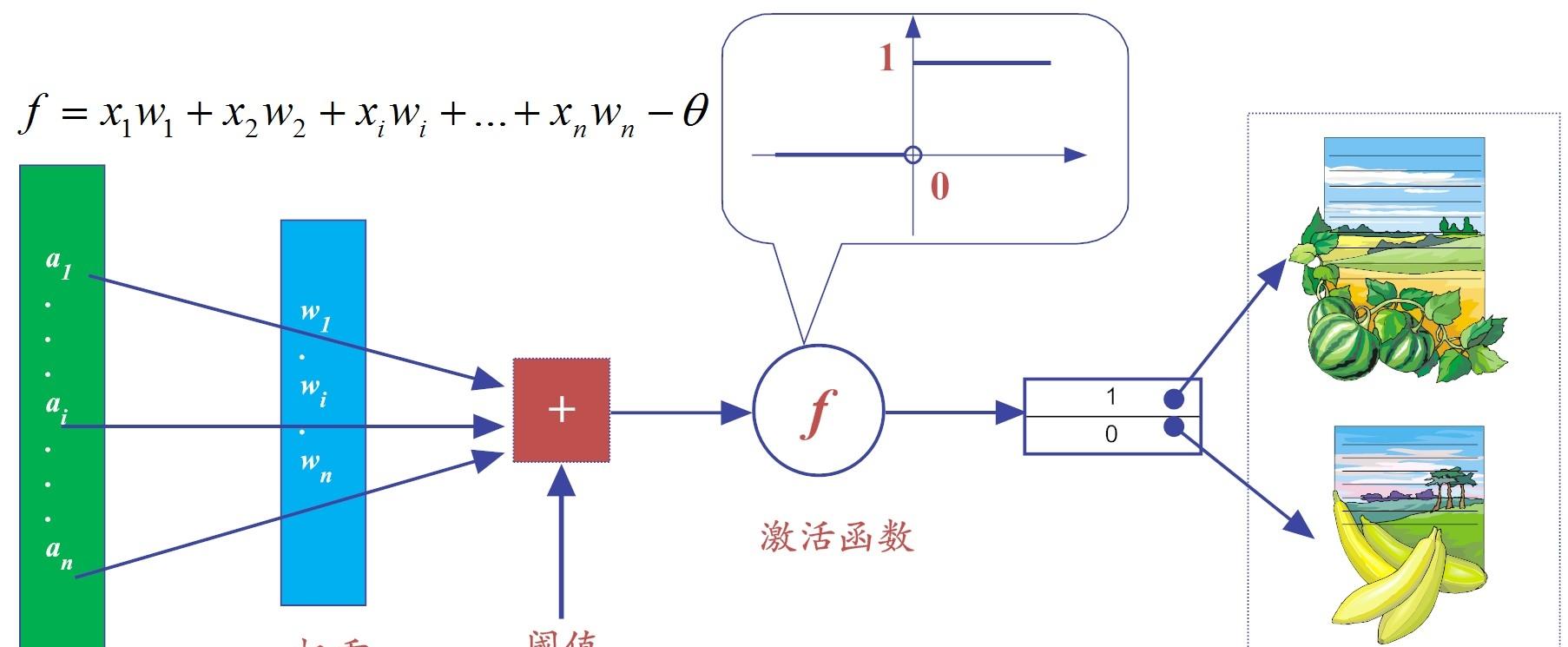
圖5-1 感覺機學習算法
假設特征x1代表輸入顔色,特征x2代表形狀,權重w1和w2預設值都為1,為了進一步簡化,我們把門檻值θ(亦有教程稱之為偏值——bias)設定為0。為了辨別友善,我們将感覺器輸出為“1”,代表判定為“西瓜”,而輸出為“0”,代表判定為“香蕉”。當然了,如果有更多類别的物品,我們就用更多的數字來标記即可。
為了友善機器計算,我們對顔色和形狀這兩個特征,給予不同的值,以示差別。比如,顔色這個特征為綠色時,x1取值為1,而當顔色為黃色時,x1取值為-1;類似地,如果形狀這個特征為圓形,x2取值為1,反之,形狀為彎曲狀時,x2取值為-1,如表5-1所示。
這樣一來,可以很容易依據圖5-1所示的公式,對于西瓜、香蕉做鑒定(即輸出函數f的值),其結果分别如圖5-2(a)所示:
圖5-2 感覺器的輸出
從圖5-2(a)所示的輸出可以看到,對西瓜的判定輸出結果是2,而香蕉的為-2。而我們先前預定的規則是:函數輸出為1,則判定為西瓜,輸出為0,則判定為香蕉,那麼如何将2或-2這樣的分類結果,變換成預期的分類表達呢,這個時候,就需要激活函數上場了!
這裡,我們使用了最為簡單的階躍函數(step function)。在階躍函數中,輸出規則非常簡單:當x>0時,f(x)輸出為1,否則輸出0。通過激活函數的“潤滑”之後,結果就變成我們想要的樣子(如圖5-2-b所示)。就這樣,我們就搞定了西瓜和香蕉的判定。
這裡需要說明的是,對象的不同特征(比如水果的顔色或形狀等),隻要用不同數值區分表示開來即可,具體用什麼樣的值,其實并無大礙。
但你或許會疑惑,這裡的門檻值(threshold)θ和兩個連接配接權值w1和w2,為啥就這麼巧分别就是0、1、1呢?如果取其它數值,會有不同的判定結果嗎?
這是個好問題。事實上,我們并不能一開始就知道這幾個參數的取值,而是一點點地非常苦逼地“折騰試錯”(try-error)出來的,而這裡的“折騰試錯”其實就是感覺機的學習過程!
下面,我們就聊聊最簡單的神經網絡——感覺機它是如何學習的?
中國有句古話:“知錯能改,善莫大焉。”說得就是“犯了錯誤而能改正,沒有比這更好的事了”。
放到機器學習領域,這句話顯然屬于“監督學習”的範疇。因為“知錯”,就表明它事先已有了事物的評判标準,如果你的行為不符合(或說偏離)這些标準,那麼就要根據“偏離的程度”,來“改善”自己的行為。
下面,我們就根據這個思想,來制定感覺機的學習規則。從前面讨論中我們已經知道,感覺機學習屬于“有監督學習”(即分類算法)。感覺機是有明确的目的導向的,這有點類似于“不管白貓黑貓,抓住老鼠就是好貓”,不管是什麼樣的學習規則,能達到良好的分類目的,就是好學習規則。
我們知道,對象本身的特征值,一旦确定下來就不會變化。是以,<b>所謂神經網絡的學習規則,就是調整權值和門檻值的規則(</b>這個結論對于深度學習而言,依然是适用的)<b>。</b>
假設我們的規則是這樣的:
其中ep
= y- y’,y為期望輸出,y’是實際輸出,是以,具體說來,ep是二者的內插補點。在後面,讀者朋友可以看到,這個“落差”就是整個網絡中權值和門檻值的調整動力。因為,很顯然,如果ep為0,那麼新、舊權值和門檻值都是一樣的,網絡就穩定可用了!
下面,我們就用上面的學習規則來模拟感覺機的學習過程。假設w1和w2初始值分别為1和-1(注意:已經不再是1和1了!),門檻值θ依然為0(事實上為其它初值,也是可行的),那麼我們遵循如下步驟,即可完成判定西瓜的學習:
(1)計算判定西瓜的輸出值f:
将這個輸出值帶入如圖5-2-b所示的階躍函數中,可得y=0。
(2)顯然,針對西瓜,我們期望輸出的正确判定是:y=1,而現在實際輸出的值y’=0,也就是說,實際輸出有誤。這個時候,就需要糾偏。而糾偏,就需要利用公式(5.1)所示的學習規則。于是,我們需要計算出來誤差ep來。
(3)計算誤差ep:
現在,我們把ep的值帶入公式(5.1)所示的規則中,更新網絡的權值和門檻值,即:
(3)那麼,在新一輪的網絡參數(即權值、門檻值)重新學習獲得後,我們再次輸入西瓜的屬性值,來測試一下,看看它能否正确判定:
再經過激活函數(階躍函數)處理後,輸出結果y=1,很高興,判定正确!
(4)我們知道,一個對象的類别判定正确,不算好,“大家好,才算真的好!”于是,在判定西瓜正确後,我們還要嘗試在這樣的網絡參數下,看看香蕉的判定是否也是正确的:
類似地,經過激活函數(階躍函數)處理後,輸出結果y=0,判定也正确的!bingo!誤差ep為0,打完收工,學習結束!
在這個案例裡,僅僅經過一輪的“試錯法(trial-by-error)”,我們就搞定了參數的訓練,但你可别高興太早,誰叫這是一個“hello world”版本的神經網絡呢!事實上,在有監督的學習規則中,我們需要根據輸出與期望值的“落差”,經過多輪重試,反複調整神經網絡的權值,直至這個“落差”收斂到能夠忍受的範圍之内,訓練才告結束。
在上面,我們僅僅給出了感覺機學習的一個感性例子,下面我們要給出感覺機學習的形式化的描述。
通過前面的分析,我們可以看到,感覺機是很容易實作邏輯上的“與(and)”、“或(or)”、“非(not)”等原子布爾函數(primitive boolean function),如圖5-3所示(睿智如你,你肯定發現了,這裡的确沒有“異或”,這個坑回頭我們在後面再填上)[2]。
圖5-3 感覺機實作邏輯運算
下面舉例說明。首先,我們注意到,假設f是如圖5-3所示的階躍函數,通過合适的權值和門檻值,即可完成常見的邏輯運算(既然是邏輯運算,x1和x2都隻能取值為0或1),例如:
(1)“與(x1∧x2)”:當權值w1=w2=1,門檻值θ=2時,有:
此時,僅當x1=x2=1時,y=1,而在其它情況下(如x1和x2無論哪一個取0),y=0。這樣,我們在感覺機中,就完成了邏輯“與”的運算。
(2)類似地,“或(x1∨x2)”:當w1=w2=1,門檻值θ=0.5時,有:
此時,當x1或x2中有一個為“1”時,那麼y=1,而在其它情況下(即x1和x2均都取“0”),y=0。這樣,我們就完成了邏輯“或”的運算。
(3)在類似地,“非(┐x1)”:當w1=0.6,w2=,0,門檻值θ=0.5時,有:
此時,當x1為“1”時,y=0,當x1為“0”時,y=1。這樣,就完成了邏輯“非”的運算(當然,如果以x2做“非”運算,也是類似操作,這裡不再贅述)。
更一般地,當我們給定訓練資料,神經網絡中的參數(權值wi和門檻值θ)都可以通過不斷地“糾偏”學習得到。為了友善起見,我們把門檻值θ視為w0,而其權值設為固定值“-1”,那麼門檻值θ就可視為一個“啞節點(dummy node)”。這樣一來,權重和門檻值的學習可以“一統天下”稱為“權重”的學習。
如此一來,感覺機的學習規則就可以更加簡單明了,對于訓練樣例(<b>x</b>,y)(需要注意的是,這裡粗體字<b>x</b>表示訓練集合),若目前感覺機的實際輸出y’,假設它不符合預期,存在“落差”,那麼感覺機的權值依據如公式(5.2)規則調整:
其中,η∈(0,1)稱為學習率(learning rate),公式(5.2)其實是公式(5.1)的一般化描述。由公式(5.2)可知,如果(<b>x</b>,y)預測正确,那麼可知y=y’,感覺機的權值就不會發生任何變化,否則就會根據“落差”的程度做對應調整。
這裡需要注意的是,學習率η的作用是“緩和”每一步權值調整強度的。它本身的大小,也是比較難以确定的。如果η太小,網絡調參的次數就太多,進而收斂很慢。如果η太大,“步子大了,容易扯着蛋”,進而錯過了網絡的參數的最優解。是以,合适的η大小,在某種程度上,還依賴于人工經驗(如圖5-4所示)。
圖5-4 學習率:“步子大了,容易扯着蛋”
如果識别對象<b>x</b>有n個特征,那麼感覺機可以看做,在n維執行個體空間(即點空間)中的超平面決策面,以向量的模式寫出來就是如圖5-5所示。
圖5-5 感覺機的超平面
這樣一來的話,對于超平面一側的執行個體,感覺機輸出為1(或稱判定為某一類),而對于超平面的另外一側執行個體,感覺機輸出為0(判定為另外一類)。
由于感覺機隻有輸出層神經元可以進行激活函數的處理,也就是說它隻擁有單層的功能元神經元(functional neuron),是以它的學習能力是相對有限的。比如說在5.4小節中,原子布爾函數中的“與、或、非”等問題都是線性可分的(linearly separable)的問題。
前面的章節中,我們提到的那位人工智能泰鬥明斯基(minsky)已經證明,若兩類模式是線性可分的,那麼一定存在一個線性超平面可以将它們區分開來,如圖5-6(a)-(c)所示。也就是說,這樣的感覺機,其學習過程一定會穩定(即收斂)下來,神經網絡的權值可以學習得到。
但是對于線性不可分原子布爾函數(如“異或”操作),就不存在簡單地線性超平面将其區分開來(如圖5-6-(d))。在這種情況下,感覺機的學習過程就會發生“震蕩(fluctuation)”,權值向量就難以求得合适解。這裡稍微為非專業讀者解釋一下什麼異或?所謂異或(xor),就是當且僅當輸入值x1和x2不相等,則輸出為1。反之,輸出為0。你可以簡單粗暴地把“異或”了解為:男歡女愛輸出為1,搞基都是沒有結果的(輸出為0)!
圖5-6 線性可分的“與、或、非”和線性不可分的“異或”
一個寄以厚望的感覺機,居然連簡單的“異或”功能都實作不了,這點讓明斯基頗為失望。于是,在1969年,他和同僚papert合作寫下《感覺機》一書[3],直接把“感覺機”判了個n年有期徒刑(n在當時為不可知變量)。
這麼一說,好像明斯基是一位法官一樣。但其實呢,他更像《白雪公主》裡的那位繼母王後。這是因為就是他,給那個叫“人工智能”的“白雪公主”喂了一顆“毒蘋果”(《感覺機》一書),讓這位“白雪公主”一睡就是20年(n=20)。
我們知道,絕大多數童話都有個“happy ending(完美結局)”,《白雪公主》也不例外。現在我們好奇的是,在人工智能領域,誰又是那位“吻醒”白雪公主的“王子”呢?
欲知後事如何,且聽我們下回分解。
在本小節,我們首先用西瓜和香蕉的判定案例,感性地談了談感覺機的工作流程。然後,我們又給出了感覺機的形式化學習規則以及感覺機的表征能力。容易發現,感覺機連常見的邏輯操作“異或”都難以實作,這一功能缺陷,直接讓人工智能領域大神明斯基抓住了“小辮子”,然後就把“人工智能”送進了長達二十年的“冬天”。
但英國浪漫主義詩人雪萊說了:“冬天來了,春天還會遠嗎?”
學習完本小節,請你思考如下問題:
(2)你知道最終感覺機是如何解決“異或”問題的嗎?(提前劇透:增加神經網絡的層數,提升網絡資料特征的表達能力,網絡層次多了,這就是深度神經網絡啊!)
寫下你的感悟,祝你每天都有收獲!
[1]
吳岸城. 神經網絡與深度學習.電子工業出版社.2016.6
[2]
周志華.機器學習.清華大學出版社.2016.2
[3] minsky
m, papert s. perceptrons[j]. 1969.
審校:我是主題曲哥哥。
<b>(未完待續)</b>
<a href="https://yq.aliyun.com/articles/96427" target="_blank">損失函數減肥用,神經網絡調權重(深度學習入門系列之六)</a>
<a href="https://yq.aliyun.com/articles/105339" target="_blank">山重水複疑無路,最快下降問梯度(深度學習入門系列之七)</a>
<a href="https://yq.aliyun.com/articles/110025" target="_blank">bp算法雙向傳,鍊式求導最纏綿(深度學習入門系列之八)</a>
<a href="https://yq.aliyun.com/articles/152935" target="_blank">全面連接配接困何處,卷積網絡見解深(深度學習入門系列之九)</a>
<a href="https://yq.aliyun.com/articles/156269" target="_blank">卷地風來忽吹散,積得飄零美如畫(深度學習入門系列之十)</a>
<a href="https://yq.aliyun.com/articles/159710" target="_blank">局部連接配接來減參,權值共享肩并肩(深度學習入門系列之十一)</a>
<a href="https://yq.aliyun.com/articles/167391" target="_blank">激活引入非線性,池化預防過拟合(深度學習入門系列之十二)</a>
<a href="https://yq.aliyun.com/articles/169880" target="_blank">循環遞歸rnn,序列模組化套路深(深度學習入門系列之十三)</a>
<a href="https://yq.aliyun.com/articles/174256" target="_blank">lstm長短記,長序依賴可追憶(深度學習入門系列之十四)</a>