本節書摘來自華章出版社《 線性代數及其應用 (原書第4版)》一書中的第2章,第2.9節,作者:(美)戴維c. 雷(david c. lay)馬裡蘭大學帕克學院 著劉深泉 張萬芹 陳玉珍 包樂娥 陸 博 譯,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
本節從坐标系的概念開始對子空間和子空間的基繼續加以讨論. 下面的定義和例子使一個有用的新術語——維數,顯得非常自然,至少對
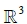
子空間是這樣.
坐标系
選擇子空間h 的一個基代替一個純粹生成集的主要原因,是 h中的每個向量可以被表示為基向量的線性組合的唯一形式. 為了明确原因,假設
是 h的基,h 中的一個向量x 可以由兩種方式生成,設
(1)
則相減得到
(2)
因為
是線性無關的,(2)中的權值必全為零. 亦即對
,(1)式中的兩種表示實際上是相同的.
定義 假設
是子空間h 的一組基,對 h中的每一個向量x ,相對于基b 的坐标是使
成立的權值
,且
中的向量
稱為 x(相對于
)的坐标向量,或x 的
-坐标向量.
例1 設
. 則因
線性無關,
是
的基. 判斷x 是否在h 中,如果是,求 x相對基
的坐标向量.
解 如果 x在 h中,則下面的向量方程是相容的:
如果數
存在,即是x 的
-坐标. 由行操作得
于是
. 基
确定 h上的一個“坐标系”,如圖2-28中的格子所示.
注意到雖然h 中的點也在
中,它們完全由屬于
中的坐标向量确定. 圖2-28中的平面上的格子使 h看起來像
. 映射
是 h和
之間保持線性組合關系的一一映射. 我們稱這種映射是同構的,且h 與
同構.
一般地,如果
是 h的基,則映射
是使h 和
的形态一樣的一一映射(盡管 h中的向量可能有多于p 個元素).(詳細的讨論見4.4節.)
子空間的維數
可以證明,若子空間 h有一組基包含 p個向量,則h 的每個基都正好包含 p個向量,(見習題27和28),于是下列定義是有意義的.
定義 非零子空間h 的維數,用 dimh表示,是h 的任意一個基的向量個數. 零子空間{0} 的維數定義為零.
空間維數為 n,
的每個基由 n個向量組成.
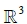
中一個經過 0的平面是2維的,一條經過 0的直線是一維的.
例2 回憶2.8節例6中矩陣 a的零空間有一個基包含3個向量. 是以這裡nul a 的維數為3. 觀察到每個基向量對應方程 ax=0的一個自由變量. 我們的構造方法總是以這種方式産生一個基. 是以,要确定nula 的維數,隻需求出 ax=0中的自由變量個數.
定義 矩陣 a的秩(記為 rank a)是a 的列空間的維數.
因為 a的主元列形成 col a的一個基,a 的秩正好是a 的主元列的個數.
例3 确定矩陣的秩
解 簡化 成階梯行:
矩陣a 有3個主元列,是以 ranka =3.
從例3的行化簡可見在 ax=0中有兩個自由變量,因為a 的五列中有兩列不是主元列. (非主元列對應于 ax=0中的自由變量.)由于主元列的個數加上非主元列的個數正好是a 的列數,col a 和 nul a的維數有如下有用的關系.(詳細内容見4.6節的秩定理.)
定理14 (秩定理)
如果一矩陣a 有 n列,則
.
下面的定理在應用中很重要,并在第5章和第6章中用到. 該定理(在4.5節中證明)當然是很顯明的,若你想到p 維子空間同構于
. 由可逆矩陣定理知,
中的 p個向量線性無關,當且僅當這 p個向量也生成
定理15 (基定理)
設 h是
的p 維子空間,h 中的任何恰好由 p個成員組成的線性無關集構成h 的一個基.并且,h 中任何生成 的p 個向量集也構成h 的一個基.
秩與可逆矩陣定理
各種與矩陣相關的向量空間的概念為可逆矩陣定理提供了更多的命題. 下面給出2.3節原定理的後續命題.
定理 (可逆矩陣定理(續))
設 a是一
矩陣,則下面的每個命題與a 是可逆矩陣的命題等價:
證 根據線性無關和生成的概念,命題(m)邏輯上與命題(e)和(h)等價. 其他五個命題通過簡單推導以如下關系與定理以前的命題相連:
命題(g)認為方程 ax=b對每一屬于
的 b有至少一個解,由此可以推出(n),因為col a 确實是所有b 的集合,滿足方程 ax=b相容的條件. 命題
是因為維數和秩的定義. 如果a 的秩是 n,即 a的列數,則根據秩定理得
,因而
. 于是有
. 同時,由命題(q)推出方程 ax=0隻有平凡解,即命題(d). 因為已知命題(d)和(g)與 是可逆矩陣的命題等價,進而定理證畢.
數值計算的注解 本教材中讨論的許多算法有助于概念的了解和手工進行簡單的計算. 然而這些算法通常不适于處理現實生活中的大規模問題.
計算秩的算法是一個很好的例子. 表面上看将矩陣簡化為階梯陣後數主元是很容易的事情. 但除非是對元素精确指定的矩陣進行算術運算,行運算可以明顯改變一個矩陣的秩. 例如,假如矩陣
中x 的值在計算機中不是存為7,那麼它的秩可能是1或2,取決于計算機是否視 x-7為零.
在實際應用中,通常使用a 的奇異值分解有效地确定矩陣 a的秩,在7.4節中将會讨論.
練習題
确定由向量
生成的
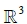
的子空間 h的維數.(首先找h 的基.)
的基
,若
,x 是什麼?
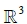
是否可能包含4維子空間?為什麼?
習題2.9
補充習題