本節書摘來自華章出版社《 線性代數及其應用 (原書第4版)》一書中的第2章,第2.6節,作者:(美)戴維c. 雷(david c. lay)馬裡蘭大學帕克學院 著劉深泉 張萬芹 陳玉珍 包樂娥 陸 博 譯,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
在wassily leontief獲得諾貝爾獎的工作中,線性代數起着重要的作用. 如第1章開始所提到的,本節所叙述的經濟模型是現在世界各國廣泛使用模型的基礎.
設某國的經濟體系分為 n個部門,這些部門生産商品和服務. 設 x為
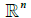
中産出向量,它列出了每一部門一年中的産出. 同時,設經濟體系的另一部分(稱為開放部門)不生産産品或服務,僅僅消費商品或服務,d 為最終需求向量,它列出經濟體系中的各種非生産部門所需求的商品或服務. 此向量代表消費者需求、政府消費、超額生産、出口或其他外部需求.
由于各部門生産商品以滿足消費者需求,生産者本身創造了中間需求,需要這些産品作為生産部門的投入,部門之間的關系是很複雜的,而生産和最後需求之間的聯系也還不清楚. 列昂惕夫思考是否存在某一生産水準x 恰好的滿足這一生産水準的總需求(x 稱為供給),那麼
{總産出x}={中間需求}+{最終需求d} (1)
列昂惕夫的投入産出模型的基本假設是,對每個部門,有一個機關消費向量,它列出了該部門的機關産出所需的投入. 所有的投入與産出都以百萬美元作為機關,而不用具體的機關如噸等(假設商品和服務的價格為常數).
作為一個簡單的例子,設經濟體系由三個部門組成——制造業、農業和服務業. 機關消費向量
如表2-1所示.
例1 如果制造業決定生産100機關産品,它将消費多少?
解 計算
為生産100機關産品,制造業需要消費制造業其他部門的50機關産品,20機關農業産品,10機關服務業産品.
若制造業決定生産
機關産出,則在生産的過程中消費掉的中間需求是
,類似地,若
和
表示農業和服務業的計劃産出,則
為它們的對應中間需求. 三個部門的中間需求為
(2)
這裡 c是消耗矩陣
,即
(3)
方程(1)和(2)産生列昂惕夫模型.
列昂惕夫投入産出模型或生産方程
(4)
把x 寫成 ix,應用矩陣代數,可把(4)重寫為
(5)
例2 考慮消耗矩陣為(3)的經濟. 假設最終需求是制造業50機關,農業30機關,服務業20機關,求生産水準x .
解 (5)中系數矩陣為
為解方程(5),對增廣矩陣作行變換
最後一列四舍五入到整數,制造業需生産約226機關,農業119機關,服務業78機關.
若矩陣 i-c可逆,則我們可應用2.2節定理5,用 i-c代替 a,由方程(i-c)x=d 得出
. 下列定理說明,在大部分的實際情況下,i-c 是可逆的,而且産出向量x 是經濟上可行的,亦即 x中的元素是非負的.
在此定理中,列的和表示矩陣中某一列元素的和. 在通常情況下,某一消耗矩陣的列的和是小于1的,因為一個部門要生産一機關産出所需投入的總價值應該小于1.
定理11 設 c為某一經濟的消耗矩陣,d 為最終需求. 若c 和 d的元素非負,c 的每一列的和小于1,則
存在,而産出向量
有非負元素,且是下列方程的唯一解
下列讨論說明定理成立的理由,且給出一種計算
的新方法.
的公式
假設由 d表示的需求在年初提供給各種工業,它們制定産業水準為x=d 的計劃,它将恰好滿足最終需求,由于這些工業準備産出為f ,它們将提出對原料及其他投入的要求. 這就創造出對投入的需求 cd.
為滿足附加需求 cd,這些工業又需要進一步的投入為
,當然,它又創造出第二輪的中間需求,當要滿足這些需求時,它們又創造出第三輪需求,即
,等等.
理論上,這個過程可無限延續下去,雖然實際上這樣一系列事件不可能一直發生下去. 我們可把這一假設的情形表示如表2-2所示.
為了滿足所有這些需求的産出水準 x是
(6)
為了使(6)有意義,我們使用下列代數恒等式:
(7)
可以證明,若 c的列的和都嚴格小于1,則 i-c是可逆的,當 m趨于無窮時
趨于0,而
.(這有點類似于當正數 小于1時,随着 m增大,
.)應用(7),我們有
當c 的列的和小于1時,
(8)
我們将(8)解釋為當 m充分大時,右邊可以任意接近于
.
在實際的投入産出模型中,消耗矩陣的幂迅速趨于0,故(8)實際上給出一種計算
的方法. 類似地,對任意d ,向量
迅速地趨于零向量,而(6)給出實際解
的方法. 若c 和d 中的元素是非負的,則(6)說明 x中的元素也是非負的.
中元素的經濟重要性
中的元素是有意義的,因它們可用來預計當最終需求 改變時,産出向量 如何改變. 事實上,
的第 j清單示當第 j個部門的最終需求增加1機關時,各部門需要增加産出的數量. 見習題8.
數值計算的注解 在任何應用問題中(不僅是經濟學)方程
總可以寫成
的形式,其中
. 若方程組很大而且稀疏(大部分元素為0),可能c 的各列元素絕對值之和小于1,這時
,若
趨向于零足夠迅速,(6)和(8)可以用來作為解方程
的實際方法,也可用來求
練習題
設某一經濟有兩個部門,商品和服務部門. 商品部門的機關産出需要0.2機關商品和0.5機關服務的投入,服務部門的機關産出需要0.4機關商品和0.3機關服務的投入. 最終需求是20機關商品和30機關服務,列出列昂惕夫投入産出模型的方程.
習題2.6