本節書摘來自華章出版社《計算機組成原理》一書中的第2章,第2.5節, 作 者 computer organization and architecture: themes and variations[英]艾倫·克萊門茨(alan clements) 著,沈 立 王蘇峰 肖曉強 譯, 更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
除了加減法,計算機還必須實作乘法和除法。這兩個操作比加減法複雜得多,所需的完成時間也長得多(或需要更複雜的硬體)。這裡僅介紹乘法和除法的基本知識。
在讨論如何進行二進制乘法之前,我們首先介紹二進制補碼數的算術移位運算。本節将其簡稱為“移位”。進行移位運算時,一個數的所有位都會向左或向右移動一位(例如,将二進制數00101100左移一位,它将變為01011000,右移一位将變為00010110)。有些計算機每次可以移動多位。
二進制補碼正數左移一位等價于将該數乘2。十進制數39的二進制表示為00100111,左移一位得到01001110,對應于十進制數78。圖2-2a描述了算術左移的過程。空出的最低位補0,移出的最高位儲存在計算機的進位标志中,進位标志在圖2-2中用c表示。進位标志是計算機中的一個位存儲單元,儲存了進位位的狀态。
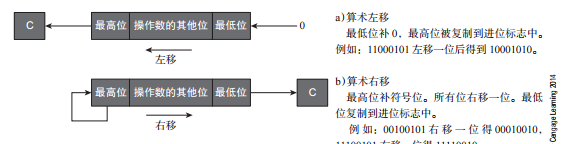
圖2-2 算術移位運算
11100011左移一位得到11000110。有符号二進制補碼數11100011表示十進制數-29。左移一位之後的結果是11000110,表示十進制數-58。
二進制數右移一位相當于它除以2。以00001100(即1210)為例,右移一位得到00000110(即610)。注意,00001101(即1310)右移一位也會得到00000110,也是610。這是因為移出的最低位被丢棄了。
負數右移需要特别注意。簡單地将二進制補碼負數11100010右移一位,結果為01110001,這顯然是不正确的。為了在移位時保持二進制補碼數的符号不變,右移時應該像圖2-2(b)那樣複制符号位。請考慮11100010(即-30)。右移一位同時保持符号位不變将得到11110001,等價于-15。
為什麼通過右移一位實作二進制補碼數除以2時要在最高位補符号位?二進制正數定義為0xxxx,…,xx,這裡x為1或0。将該數除以2,會得到00pppp,…, pp。這個數的補數為1yyyy,…, yy+1(這裡每個y是對應的x的補)。現在把00pppp,…, pp轉換為負數,會得到11qqqq,…, qq+1。正如我們所看到的那樣,無論是正數還是負數,右移時符号位都應保持不變。
請回顧人們在紙上筆算兩個數乘法的過程。這裡之是以強調人們是因為計算機不會像人那樣進行乘法運算——它是将所有部分積加到一起。計算機從乘數的最低位開始,每次檢查一位,判斷它是否為0。如果乘數的目前位為1則寫下被乘數,若該位為0則寫下n個0。接下來檢查乘數的下一位,但這時應從上一個數的左邊一位開始寫下被乘數(或0)。被寫下的這一組數叫作部分積。在得到所有的部分積之後,将它們加到一起,得到乘法的結果。
乘法的結果100000102 = 13010是個8位二進制數。兩個n位二進制數相乘會得到一個2n位的積。正如前面提到的那樣,數字計算機并沒有實作上面的算法,因為這種算法要求計算機存儲n個部分積,然後将它們同時相加。一種更好的技術是每得到一個部分積時就做一次加法。圖2-3給出了一個計算兩個n位無符号二進制數相乘的算法。請考慮用圖2-3描述的算法計算1101 × 1010的例子。表2-3給出了其計算過程。
這種通過移位和加法實作的乘法速度很慢。實際的計算機采用了多種方法加快乘法運算的速度。例如,構造專門的邏輯陣列直接得到兩個數的積而不必對操作數移位。
有些程式員使用移位和加法等速度相對較快的操作以避免使用乘法。請考慮p乘以10和乘以9這兩個例子。
10p = 2×(2×2×p + p);即将p左移兩次,加上p,再将和左移一次。
9p = 2×2×2×p + p;即将p左移三次,加上p得到結果。
乘法運算也可以借助查找表(look-up table)實作,這種方法将兩個數相乘所有可能的積都儲存在一個隻讀存儲器内。這樣,隻需簡單地用x和y的值找到表中的對應項就可以得到x和y的乘積。例如,兩個8位二進制數乘法需要一個16位位址(即兩個8位字)、216項的查找表,每項記錄了一個16位的積。計算00001010乘以00111100的積隻需讀出位址為0000101000111100的項的内容00000010010110000。
這種方法的缺點在于所需rom的容量随着乘數和被乘數位數的增加呈指數增長。n位乘法需要的rom容量為2n×22n位;例如8位乘法需要容量為16×216位的rom。
可以用一個簡單的方法來減少查找表的大小。假設要計算兩個16位數a與b的乘積。可以将16位數a拆分為兩個8位數au和al,這裡au是a的高8位而al是a的低8位。如果a=1111000010101010,則au=11110000,al=10101010。a可被表示為au×256+al,b可被表示為bu×256+bl。現在,請考慮乘積a×b。
a×b=(au×256+al)×(bu×256+bl)=65536aubu+256aubl+256albu+albl
這個表達式需要計算4個8位乘積(aubu,albu,aubl,albl),将積左移16位或8位(即乘以65536或256),以及将4個部分積相加等操作。這樣,可以用8位乘法和4個加法來完成16位乘法。實際上,借助硬體有很多辦法可以加快乘法運算的速度。
除法是通過被除數不斷地減去除數直到結果為零或小于除數來實作的。減去除數的次數稱作“商(quotient)”,最後一次減法的差稱作“餘數(remainder)”。也就是說,
被除數/除數 = 商 + 餘數/除數
在讨論二進制除法之前,我們首先看看人們在紙上筆算完成十進制除法的過程。下面的算式描述了575除以25的過程。
第一步是比較除數和被除數的最高兩位,看看被除數的最高兩位中有幾個除數。這個例子中答案為2(即2×25 = 50),并用57減去2×25。在商的最高位上寫下數字2,得到下面的算式。
将被除數的下一個數字5移下到7的後面,并比較除數和75。由于75正好是25的整倍數,是以應在商的下一位上寫下數字3并得到
因為已經處理到被除數的最後一位且75正好是除數的整倍數,是以除法結束,商為23,餘數為0。上述除法過程的難點在于估計部分被除數中有多少個除數(即57除以25等于2餘7)。請考慮用無符号二進制除法完成同樣的例子。
被除數的前5位比除數小,是以商的最高位商0并将除數與被除數的前6位比較。
被除數的前6位中有一個除數,減法後得到新的部分被除數為001010(1111)。将被除數的下一位移下來,可得
新的部分被除數小于除數,是以商的下一位商0。後續的除法過程如下:
除法結果商為10111,餘數為0。
1.恢複餘數除法
稍加改動,剛才讨論的除法方法就可以以數字形式實作。唯一需要修改的就是除數與部分被除數的比較方法。人們用心算進行比較,而計算機必須做減法并檢測結果的符号位。如果減法的結果為正,則商1,但若結果為負,則應商0并将部分被除數與除數相加,将其恢複為原先的值。
下面是一個可行的恢複餘數除法算法。
1)将除數的最高位與被除數的最高位對齊。
2)從部分被除數中減去除數,得到新的部分被除數。
3)若新的部分被除數為負,則商0并用新的部分被除數加上除數,恢複原先的部分被除數。
4)若新的部分被除數為負,則商1。
5)判斷除法是否結束。若除數的最低位與部分被除數的最低位對齊,則除法結束。最後的部分被除數就是餘數。否則,執行第6步。
6)将除數右移1位。從第2步繼續執行。
圖2-4描述了該算法的流程圖。下面按照該流程計算011001112除以10012,即十進制數103除以9,其結果為商11餘4。表2-5逐漸列出了除法的過程。
2.不恢複餘數除法
改進圖2-4中的恢複餘數除法可以減少除法的延遲。不恢複餘數除法與恢複餘數法基本相同,唯一的差別在于它取消了恢複餘數的操作。在恢複餘數除法中,在部分被除數與除數相加恢複部分被除數之後的一個周期,部分被除數将減去除數的二分之一。每個将除數右移的操作等價于将除數除以2。目前周期恢複部分被除數以及下個周期減去除數一半的操作等價于部分被除數加上除數的一半。即d - d/2 = +d/2,這裡d為除數。
圖2-5給出了不恢複餘數除法的流程圖。部分被除數減去除數之後,将檢測新的部分被除數的符号位。若為負,則商左移1位,商的最低位補0,并将部分被除數加上除數的二分之一。若為正,則商左移1位,商的最低位補1,并将部分被除數減去除數的二分之一。表2-6列出了用不恢複餘數除法完成表2-5中算例的過程。