目錄
簡介
密鑰推導函數key derivation function
Password Hashing Competition
Argon2算法
Argon2的輸入參數
處理流程
簡介
Argon2是一個密鑰推導函數,在2015年7月被選為密碼哈希大賽的冠軍,它由盧森堡大學的Alex Biryukov、Daniel Dinu和Dmitry Khovratovich設計,Argon2的實作通常是以Creative Commons CC0許可(即公共領域)或Apache License 2.0釋出,并提供了三個相關版本,分别是Argon2d,Argon2i和Argon2id。
本文将會讨論一下Argon2的原理和使用。
密鑰推導函數key derivation function
在密碼學中,密鑰推導函數(KDF)是一種密碼學哈希函數,它使用僞随機函數從一個秘密值(如主密鑰、密碼或密碼)中推導出一個或多個密鑰。 KDF可用于将密鑰拉伸成更長的密鑰,或獲得所需格式的密鑰,例如将Diffie-Hellman密鑰交換的結果轉換為用于AES的對稱密鑰。
Password Hashing Competition
密碼學雖然是研究密碼的,但是其加密算法是越公開越好,隻有公開才能去檢視該算法的好壞,隻有經過大家的徹底研究,才能夠讓該算法得以在業界使用和傳播。
最出名的密碼算法大賽肯定是由NIST在2001年為了指定标準的AES算法舉辦的大賽,該大賽的目的尋找最新的加密算法來替代老的DES算法。在這次大賽中,湧現了許多優秀的算法,包括CAST-256, CRYPTON, DEAL, DFC, E2, FROG, HPC, LOKI97, MAGENTA, MARS, RC6, Rijndael, SAFER+, Serpent, 和 Twofish等。最終Rijndael算法被選為最終的AES算法實作。
同樣的PHC也是一個這樣的算法比賽,和NIST舉辦的算法比賽不同的是,這是一個非官方的,由密碼學家們組織的比賽。它是在由Jean-Philippe Aumasson于2012年秋季發起。
2013年第一季度,釋出了征集意見書的通知,到2014年3月31日截止日期,共收到24份意見書。2014年12月,确定了9個入圍名單。2015年7月,宣布Argon2為優勝者。
Argon2算法
Argon2 的設計很簡單,旨在實作最高的記憶體填充率和對多個計算單元的有效利用,同時還能提供對 tradeoff attacks 的防禦(通過利用處理器的緩存和記憶體)。
Argon2有三個變種。Argon2i、Argon2d和Argon2id。Argon2d速度更快,并且使用資料依賴的記憶體通路方式,這使得它對GPU破解攻擊有很強的抵抗力,适合沒有side-channel timing attacks威脅的應用(例如加密貨币)。
Argon2i則使用資料無關的記憶體通路,這對于密碼哈希和基于密碼的密鑰推導算法來說是首選,其特點是速度較慢,因為它在記憶體上運作了更多的處理邏輯,以防止 tradeoff attacks 。
Argon2id是Argon2i和Argon2d的混合體,采用資料依賴型和資料獨立型記憶體通路相結合的方式,進而可以同時抵禦side-channel timing attacks和GPU破解攻擊的能力。
Argon2有兩類輸入參數,分别是primary inputs和secondary inputs。
primary inputs包括要加密的消息P和nonce S,分别代表password和salt。
P的長度是0到232-1位元組,S的長度是8到232-1位元組(如果是做密碼hash,推薦16位元組)。
之是以叫做primary inputs,是因為這兩個參數是必須輸入的。
剩下的參數叫做secondary inputs,他們包括:
并行程度p,表示同時可以有多少獨立的計算鍊同時運作,取值是1到224-1。
Tag長度 τ, 長度從4到232-1位元組。‘
記憶體大小 m, 機關是兆,值取 8p到232-1。
疊代器的個數t,提升運作速度。取值1到232-1。
版本号v,一個位元組,取值0x13。
安全值 K , 長度是0到232-1位元組。
附加資料 X,長度是0到232-1位元組。
Argon2的類型,0代表Argon2d,1代表Argon2i,2代表Argon2id。
這些輸入可以用下面的代碼來表示:
我們先來看一下非并行的Argon2的算法流程:
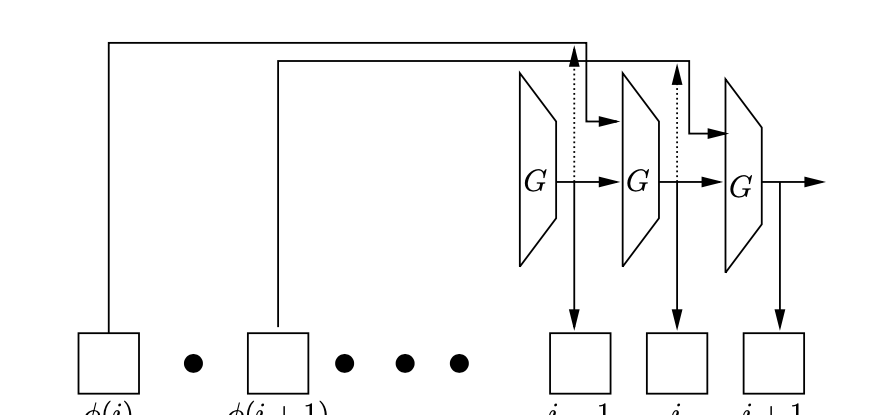
非并行的Argon2是最簡單的。
上圖中G表示的是一個壓縮函數,接收兩個1024byte的輸入,輸出一個1024byte。
i表示的是執行的步數,上面的φ(i) 就是輸入,取自記憶體空間。
作為一個memory-hard的算法,一個很重要的工作就是建構初始記憶體。接下來,我們看一下如何建構初始記憶體空間。
首先,我們需要建構 H0 ,這是一個 64-byte 的block值,通過H0,可以去建構更多的block。計算H0的公式如下:
H0 = H(p,τ,m,t,v,y,⟨P⟩,P,⟨S⟩,S,⟨K⟩,K,⟨X⟩,X)
它是前面我們提到的輸入參數的H函數。H0的大小是64byte。
看下H0的代碼生成:
對于輸入參數并行程度p來說,需要将記憶體分成一個記憶體矩陣<code>B[i][j]</code>, 它是一個 p 行的矩陣。
計算矩陣B的值:
其中H′ 是一個基于H的變長hash算法。
我們給一下這個算法的實作:
如果我們的疊代次數多于一次,也就是說t > 1, 我們這樣計算下一次疊代的 B :
\(B^{t}[i][0]=G\left(B^{t-1}[i][q-1], B\left[i^{\prime}\right]\left[j^{\prime}\right]\right) \oplus B^{t-1}[i][0]\)
\(B^{t}[i][j]=G\left(B^{t}[i][j-1], B\left[i^{\prime}\right]\left[j^{\prime}\right]\right) \oplus B^{t-1}[i][j]\)
最終周遊T次之後,我們得到最終的B :
\(B_{\text {final }}=B^{T}[0][q-1] \oplus B^{T}[1][q-1] \oplus \cdots \oplus B^{T}[p-1][q-1]\)
最後得到輸出:
\(\mathrm{Tag} \leftarrow H^{\prime}\left(B_{\text {final }}\right)\)
這段邏輯也可以用代碼來表示: