堆是一個數組,可以被看成一個近似的完全二叉樹。 樹上的每一個結點對應數組中的一個元素
A[1...A.heap-size]
PARENT(i) return Li/2j
LEFT 2i
RIGHT 2i + 1
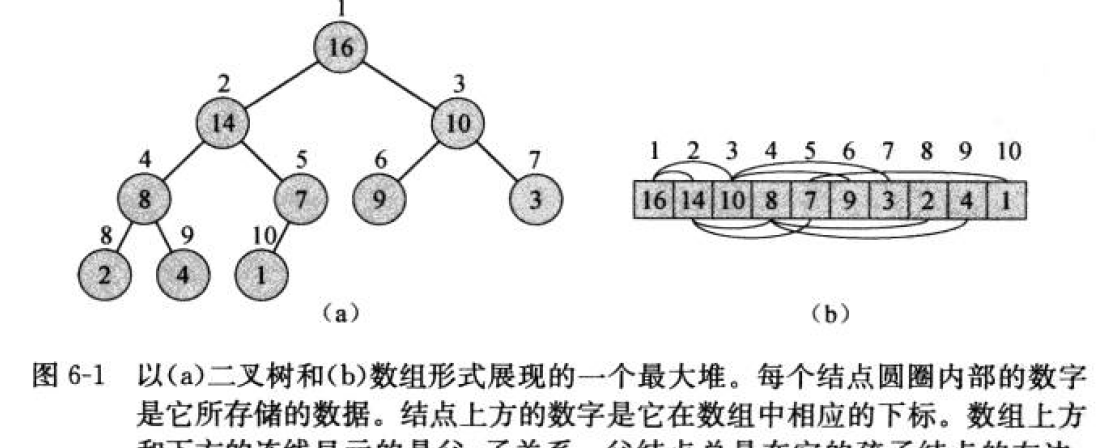
最大堆的性質 A[PARENT(i)] >= A[i]
最小堆的性子 A[PARENT(i)] <= A[i]
MAX-HEAPIFY o(lgn) 維護最大堆
BUILD-MAX-HEAP 線性時間複雜度
HEAPSORT o(n*lgn)
MAX-HEAP-INSERT, HEAP-EXPACT-MAX, HEAP-INCREASE-KEY, HEAP-MAXIMUM
MAX-HEAPIFY(i)
l = LEFT(i)
r = RIGHT(i)
if l <= A.heap-size and A[l] > A[i]
largest = l
else largest = i
if r <= A.heap-size and A[r] > A[i]
largeset = r
if largest != i
exchange A[i] with A[largest]
MAX-HEAPIFY(largest)
建堆
BUILD-MAX-HEAP(A)
A.heap-size = A.length
for i = LA.length/2J downto 1MAX-HEAPIFY(A, i)
堆排序算法
HEAPSORT(A)
for i = A.length donwto 2
exchange A[1] with A[i]
A.heap-size = A.heap-size -1
MAX-HEAPIFY(A,1)
利用BUILD-MAX-HEAP(A)将輸入數組A[1...A.length]建成最大堆 因為數組最大元素總在根A[1] , 通過它與A[n] 進行交換,我們可以讓該元素放到正确位置。如果我們從堆中去掉n 剩餘節點中
根的孩子仍然是最大堆,而新的根節點可能違背最大堆的性質。為了維護最大堆的性子,我們調用MAX-HEPIFY(A,1)
優先隊列
INSERT(S, x)
MAXIMUM(S)
EXTRACT-MAX(S)
INCREASE-KEY(S, x, k)
用堆來實作優先隊列,需要在堆中的每個元素裡存儲對對象的句柄
HEAP-MAXIMUM
return A[1]
HEAP-EXTRACT-MAX(S)
if A.heap-size < 1
error "heap underflow"
max = A[1]
A[1] = A[A.heap-size]
A.heap-size = A.heap-size - 1
MAX-HEAPIFY(A,1)
return max
HEAP-INCREASE-KEY(A, i, key)
if key < A[i]
error "new key is smaller than current key"
A[i] = key
while i > 1 and A[PARENT(i)] < A[i]
exchange A[i] with A[PARENT(i)]
i = PARENT(i)
MAX-HEAP-INSERT(A, key)
A.heap-size = A.heap-size + 1
A[A.heap-size] = -OO
HEAP-INCREASE-KEY(A, A.heap-size, key)
本文轉自莫水千流部落格園部落格,原文連結:http://www.cnblogs.com/zhoug2020/p/6160283.html,如需轉載請自行聯系原作者