TYVJ-P1035 棋盤覆寫

​​題目傳送門​​

我們選擇33的網格進行讨論

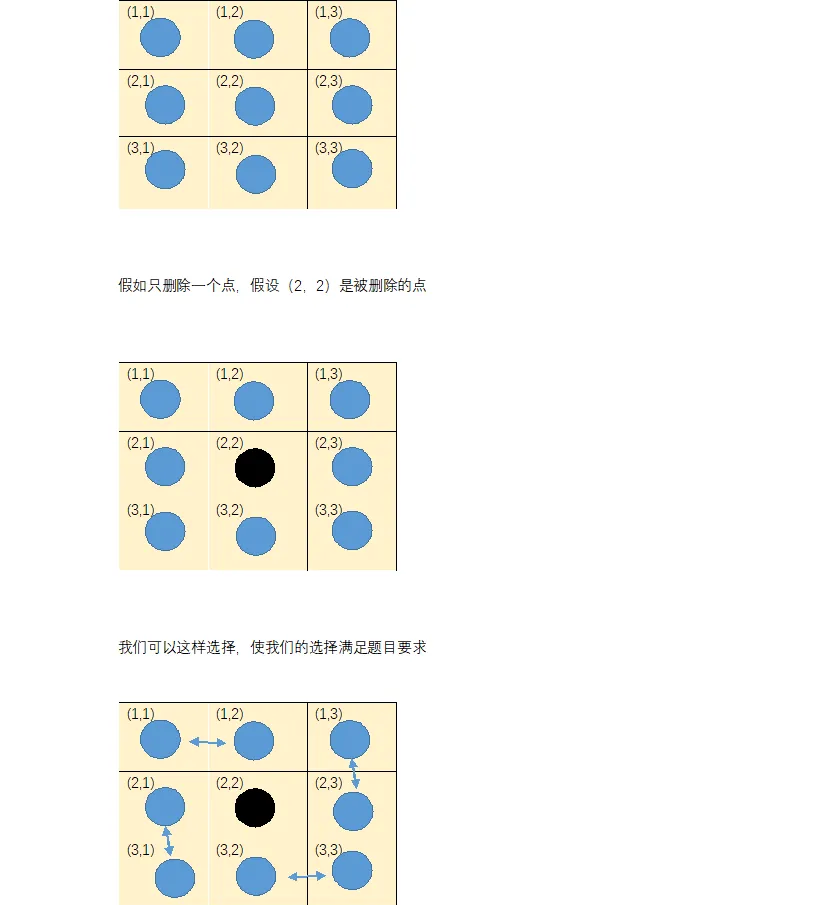
有沒有發現，因為每個點隻能掩蓋一次，是以題目要求的就是一個二分圖最大比對對數，因為要選擇12的多米諾骨牌進行掩蓋，不就是選擇兩個格子嗎？這樣的話，題目不就是要選擇最多的這樣的兩個格子進行掩蓋嗎？這樣的？什麼樣子的兩個格子呢？當然是上下左右相臨的啊，是以建圖就不難了吧。

#include<cstdio>
#include<cstring>
using namespace std;
int n,m;
int x[4]={0,0,1,-1};
int y[4]={-1,1,0,0};
bool map[101][101];
int link[10010];
bool used[10010];
int head[10010],cnt;
struct TT
{
    int v,next;
}edge[50000];
void addedge(int u,int v)
{
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
bool can(int t)
{
    for(int p=head[t];p!=-1;p=edge[p].next)
    {
        int v=edge[p].v;
        if(used[v]==false)
        {
            used[v]=1;
            if(link[v]==-1||can(link[v]))
            {
                link[v]=t;
                return true;
            }
        }
    }
    return false;
}
int MaxMatch()
{
    int num=0;
    memset(link,-1,sizeof(link));
    for(int i=1;i<=n*n;i++)
    {
        memset(used,false,sizeof(used));
        if(can(i)) num++;
    }
    return num;
}
int main()
{
    cnt=0;
    memset(head,-1,sizeof(head));
    memset(map,false,sizeof(map));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        map[x][y]=true;
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
      if(!map[i][j])
      {
          int num=(i-1)*n+j;
          for(int k=0;k<4;k++)
          {
              int xx=i+x[k];
              int yy=j+y[k];
         if(xx>=1&&xx<=n&&yy>=1&&yy<=n&&!map[xx][yy])
              {
                  int numb=(xx-1)*n+yy;
                  addedge(num,numb);
              }
          }
      }
    printf("%d\n",MaxMatch()/2);
    return 0;
}