文章首發公衆号: bigsai
前言
hello,大家好,我是bigsai哥哥,好久不見,甚是想念哇🤩!
今天給大家分享一個TOPK問題,不過我這裡不考慮特别大分布式的解決方案,普通的一道算法題。
首先搞清楚,什麼是topK問題?
topK問題,就是找出序列中前k大(或小)的數,topK問題和第K大(或小)的解題思路其實大緻一緻的。
TopK問題是一個非常經典的問題,在筆試和面試中出現的頻率都非常非常高(從不說假話)。下面,從小小白的出發點,認為topK是求前K大的問題,一起認識下TopK吧!
目前,在求TopK和第K大問題解法差不多,這裡就用力扣215數組的第k個大元素 作為解答的題示範啦。看這篇之前,可以看我的這篇程式員必知必會的十大排序 先對各個排序有所了解才行。
排序法
找到TopK,并且排序TopK
啥,你想要我找到TopK?不光光TopK,你想要多少個,我給你多少個,并且還給你排序給排好,啥排序我最熟悉呢?
如果你想到冒泡排序O(n^2)那你就大意了啊。
如果使用O(n^2)級别的排序算法,那也是要優化的,其中冒泡排序和簡單選擇排序,每一趟都能順序确定一個最大(最小)的值,是以不需要把所有的資料都排序出來,隻需要執行K次就行啦,是以這種算法的時間複雜度也是O(nk)。
這裡給大家回顧一下冒泡排序和簡單選擇排序差別:
冒泡排序和簡單選擇排序都是多趟,每趟都能确定一個最大或者最小,差別就是冒泡在枚舉過程中隻和自己後面比較,如果比後面大那麼就交換;而簡單選擇是每次标記一個最大或者最小的數和位置,然後用這一趟的最後一個位置數和它交換(每一趟确定一個數枚舉範圍都慢慢變小)。
下面用一張圖表示過程:
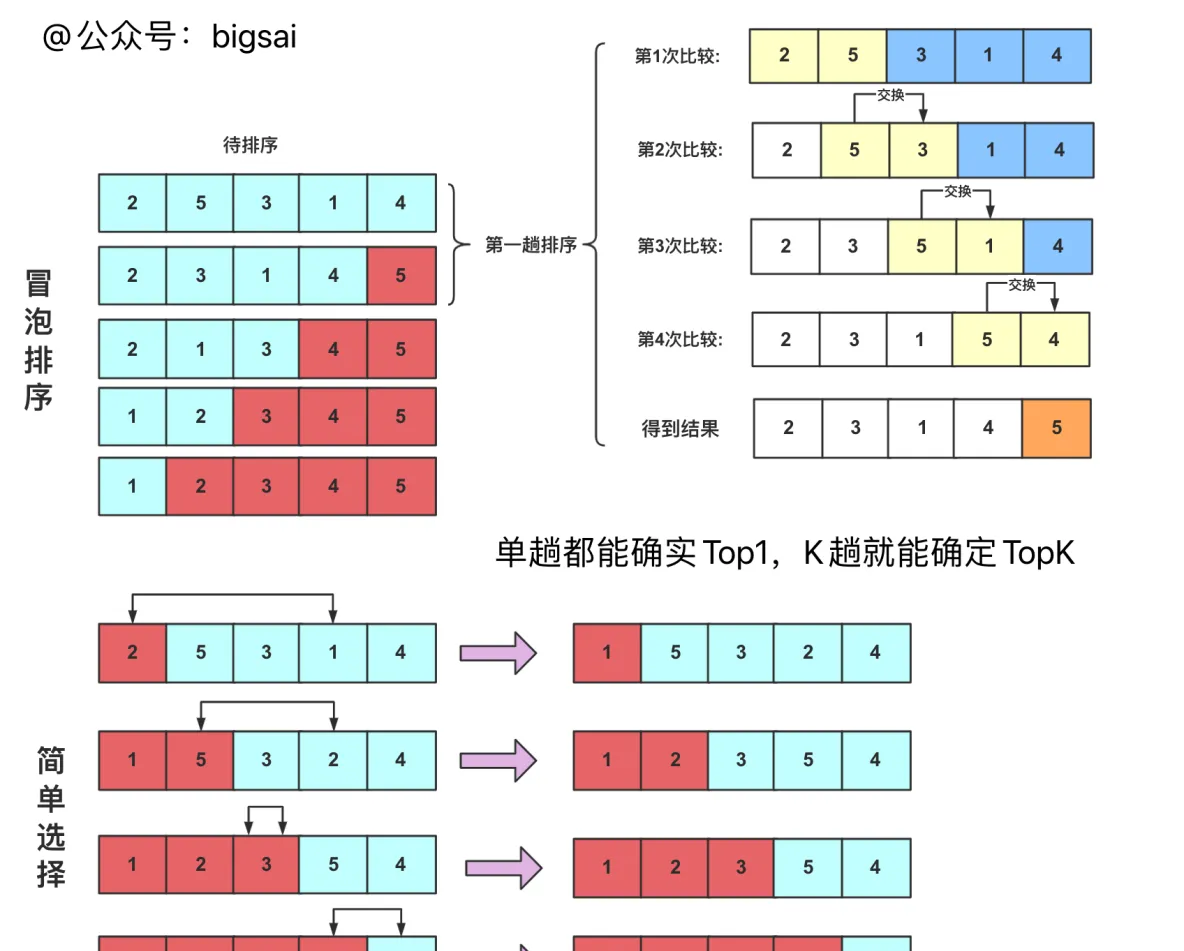
這裡把code也給大家提供一下,簡單選擇上面圖給的是每次選最小,實作的時候每次選最大就可以了。
//交換數組中兩位置元素
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//冒泡排序實作
public int findKthLargest1(int[] nums, int k) {
for(int i=nums.length-1;i>=nums.length-k;i--)//這裡也隻是k次
{
for(int j=0;j<i;j++)
{
if(nums[j]>nums[j+1])//和右側鄰居比較
{
swap(nums,j,j+1);
}
}
}
return nums[nums.length-k];
}
//簡單選擇實作
public int findKthLargest2(int[] nums, int k) {
for (int i = 0; i < k; i++) {//這裡隻需要K次
int max = i; // 最小位置
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] > nums[max]) {
max = j; // 更換最小位置
}
}
if (max != i) {
swap(nums, i, max); // 與第i個位置進行交換
}
}
return nums[k-1];
} 當然,快排和歸并排序甚至堆排序也可以啊,這些排序的時間複雜度為O(nlogn),也就是将所有資料排序完然後直接傳回結果,這部分就不再詳細講解啦,調調api或者手寫排序都可。
兩種思路的話除了K極小的情況O(nk)快一些,大部分情況其實還是O(nlogn)情況快一些的,不過從O(n^2)想到O(nk),還是有所收獲的。
基于堆排優化
這裡需要知道堆相關的知識,我以前寫過優先隊列和堆排序,這裡先不重複講,大家也可以看一下:
優先隊列不知道,看看堆排序吧
硬核,手寫一個優先隊列
上面說道堆排序O(nlogn)那是将所有元素都排序完然後取前k個,但是其實上我們分析一下這個堆排序的過程和幾個注意點哈:
堆這種資料結構,分為大根堆和小根堆,小根堆是父節點值小于子節點值,大根堆是父節點的值大于子節點的值,這裡肯定是要采用大根堆的。
堆看起來是一個樹形結構,但是堆是個完全二叉樹我們用數組存儲效率非常高,并且也非常容易利用下标直接找到父子節點,是以都用數組來實作堆,每次排序完成的節點都将數移到數組末尾讓一個新數組組成一個新的堆繼續。
堆排序從大的來看可以分成兩個部分,無序數組建堆和在堆基礎上每次取對頂排序。其中無序數組建堆的時間複雜度為O(n),在堆基礎上排序每次取堆頂元素,然後将最後一個元素移到堆頂進行調整堆,每次隻需要O(logn)級别的時間複雜度,完整排序完n次就是O(nlogn),但是咱們每次隻需要k次,是以完成k個元素排序功能需要花費O(klogn)時間複雜度,整個時間複雜度為O(n+klogn)因為和前面區分一下就不合并了。
畫了一張圖幫助大家了解,進行兩次就獲得Top2,進行k次就獲得TopK了。
實作代碼為:
class Solution {
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
//下移交換 把目前節點有效變換成一個堆(大根)
public void shiftDown(int arr[],int index,int len)//0 号位置不用
{
int leftchild=index*2+1;//左孩子
int rightchild=index*2+2;//右孩子
if(leftchild>=len)
return;
else if(rightchild<len&&arr[rightchild]>arr[index]&&arr[rightchild]>arr[leftchild])//右孩子在範圍内并且應該交換
{
swap(arr, index, rightchild);//交換節點值
shiftDown(arr, rightchild, len);//可能會對孩子節點的堆有影響,向下重構
}
else if(arr[leftchild]>arr[index])//交換左孩子
{
swap(arr, index, leftchild);
shiftDown(arr, leftchild, len);
}
}
//将數組建立成堆
public void creatHeap(int arr[])
{
for(int i=arr.length/2;i>=0;i--)
{
shiftDown(arr, i,arr.length);
}
}
public int findKthLargest(int nums[],int k)
{
//step1建堆
creatHeap(nums);
//step2 進行k次取值建堆,每次取堆頂元素放到末尾
for(int i=0;i<k;i++)
{
int team=nums[0];
nums[0]=nums[nums.length-1-i];//删除堆頂元素,将末尾元素放到堆頂
nums[nums.length-1-i]=team;
shiftDown(nums, 0, nums.length-i-1);//将這個堆調整為合法的大根堆,注意(邏輯上的)長度有變化
}
return nums[nums.length-k];
}
} 基于快排優化
上面堆排序都能優化,那麼快排呢?
快排當然能啊,這麼牛的事情怎麼能少得了我快排呢?
這部分需要堆快排有一定了解和認識,前面很久前寫過:圖解手撕冒泡和快排 (後面待優化),快排的核心思想就是:分治 ,每次确定一個數字的位置,然後将數字分成兩個部分,左側比它小,右側比它大,然後遞歸調用這個過程。每次調整的時間複雜度為O(n),平均次數為logn次,是以平均時間複雜度為O(nlogn)。
但是這個和求TopK有什麼關系呢?
我們求TopK,其實就是求比目标數字大的K個,我們随機選一個數字例如上面的5,5的左側有4個,右側有4個,可能會出現下面幾種情況了:
① 如果k-1等于5右側數量,那麼說明中間這個5就是第K個,它和它的右側都是TopK。
②如果k-1小于5右側數的數量 ,那麼說明TopK全在5的右側,那麼可以直接壓縮空間成右側繼續遞歸調用同樣方法查找。
③ 如果k-1大于5右側的數量,那麼說明右側和5全部在TopK中,然後左側還有(k-包括5右側數總數),此時搜查範圍壓縮,k也壓縮。舉個例子,如果k=7 那麼5和5右側已經占了5個數字一定在Top7中,我們隻需要在5左側找到Top2就行啦。
這樣一來每次數值都會被壓縮,這裡因為快排不是完全遞歸,時間複雜度不是O(nlogn)而是O(n)級别(詳細的可以找一些網上證明),但是測試樣例有些極端代碼比如給你跟你有序1 2 3 4 5 6…… 找Top1 就出現比較極端的情況。是以具體時候會用一個随機數和第一個交換一下防止特殊樣例(僅僅為了刷題用的),當然我這裡為了就不加随機交換的啦,并且如果這裡要得到的TopK是未排序的。
詳細邏輯可以看下實作代碼為:
class Solution {
public int findKthLargest(int[] nums, int k) {
quickSort(nums,0,nums.length-1,k);
return nums[nums.length-k];
}
private void quickSort(int[] nums,int start,int end,int k) {
if(start>end)
return;
int left=start;
int right=end;
int number=nums[start];
while (left<right){
while (number<=nums[right]&&left<right){
right--;
}
nums[left]=nums[right];
while (number>=nums[left]&&left<right){
left++;
}
nums[right]=nums[left];
}
nums[left]=number;
int num=end-left+1;
if(num==k)//找到k就終止
return;
if(num>k){
quickSort(nums,left+1,end,k);
}else {
quickSort(nums,start,left-1,k-num);
}
}
} 計數排序番外篇
排序總有一些騷操作的排序—線性排序,那麼你可能會問桶類排序可以嘛?
也可以啦,不過要看數值範圍進行優化,桶類排序适合資料均勻密集出現次數比較多的情況,而計數排序更是希望數值能夠小一點。
那麼利用桶類排序的具體核心思想是怎麼樣的呢?
先用計數排序統計各個數字出現次數,然後将新開一個數組從後往前疊加求和計算。
這種情況非常适合數值巨量并且分布範圍不大的情況。
代碼本來不想寫了,但是念在你會給我三連我寫一下吧
//力扣215
//1 <= k <= nums.length <= 104
//-104 <= nums[i] <= 104
public int findKthLargest(int nums[],int k)
{
int arr[]=new int[20001];
int sum[]=new int[20001];
for(int num:nums){
arr[num+10000]++;
}
for(int i=20000-1;i>=0;i--){
sum[i]+=sum[i+1]+arr[i];
if(sum[i]>=k)
return i-10000;
}
return 0;
} 結語
好啦,今天的TopK問題就到這裡啦,相信你下次遇到肯定會拿捏它。
TopK問題不難,就是巧妙利用排序而已。排序是非常重要的,面試會非常高頻。
這裡我就不藏着掖着攤牌了,以面試官的角度會怎麼引導你說TOPK問題。
狡猾的面試官:
嗯,我們來聊聊資料結構與算法,來講講排序吧,你應該接觸過吧?講出你最熟悉的三種排序方式,并講解一下其中具體算法方式。
卑微的我:
bia la bia la bia la bia la……