導讀
本文主要介紹OpenCV基于相位相關的圖像拼接方法與示範。
OpenCV圖像拼接相關文章
了解OpenCV圖像拼接常用方法可以點選下面标題進入對應往期文章介紹:
- OpenCV常用圖像拼接方法(一):直接拼接(硬拼)
- OpenCV常用圖像拼接方法(二):基于模闆比對拼接
- OpenCV常用圖像拼接方法(三):基于特征比對拼接
- OpenCV常用圖像拼接方法(四):基于Stitcher類拼接
OpenCV圖像拼接終章--Stitching detailed使用與參數介紹
相位相關簡介
相位相關(phase correlate)可以用于檢測兩幅内容相同的圖像之間的相對位移量。可用于對齊圖像,不具備光照不變性。它是基于傅立葉變換的位移定理:一個平移過的函數的傅立葉變換僅僅是未平移函數的傅立葉變換與一個具有線性相位的指數因子的乘積,即空間域中的平移會造成頻域中頻譜的相移。它的公式定義為:設二維函數(圖像)f(x,y)的傅立葉變換為F(u,v),即DFT[f(x,y)]=F(u,v),如果f(x,y)平移(a,b),則平移後的傅立葉變換為:
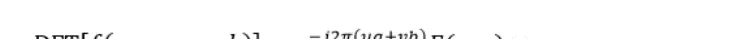
是以,當兩幅函數f1(x,y)和f2(x,y)僅僅有位移的差異,即f2(x,y)= f1(x-a,y-b),則它們的傅立葉變換F1(u,v)和F2(u,v)有如下關系:
由上式很容易得到f1(x,y)和f2(x,y)的互功率譜為(這裡還用到了f1(x,y)和f2(x,y)的頻譜的模相等):
式中F*表示F的共轭,上式表示平移定理保證了互功率譜的相位等于兩幅圖像之間的相移。
Opencv的文檔給出了詳細的用相位相關法求解位移量的過程:
[1] 對待處理的兩幅圖像src1和src2應用窗函數去除圖像的邊界效應,文檔中推薦使用漢甯窗,它可用createHanningWindow函數生成;
[2] 求傅立葉變換:Ga=DFT[scr1]和Ga=DFT[scr1];
[3] 計算互功率譜;
[4] 對互功率譜求傅立葉逆變換:r=DFT-1[R];
[5] 對r計算最大值的位置,并在以該位置為中心的5×5的窗體内應用下列公式獲得亞像素級的精度位置:
最終(a,b)為兩個圖像之間的位移量。
OpenCV相位相關函數
OpenCV相位相關函數phaseCorrelate:
參數:
| src1 | 輸入浮點圖像1 CV_32FC1 或 CV_64FC1 |
| src2 | 輸入浮點圖像2 CV_32FC1 或 CV_64FC1,與src1相同寬高 |
| window | 帶加窗系數的浮點數組以減少邊緣效應(可選) |
| response=0 | 峰值周圍5x5質心内的信号功率,介于0和1之間(可選) |
| 傳回值 | 檢測到兩個陣列之間的相移(亞像素級别) |
基于相位相關圖像拼接
本文使用的拼接圖像從下圖中截取兩部分,分别儲存為01.jpg(待拼接左圖)和02.jpg(待拼接右圖)
01.jpg(待拼接左圖)
02.jpg(待拼接右圖)
相位相關函數傳回結果:
Point2d shiftPt = phaseCorrelate(grayL64F, grayR64F);
cout << shiftPt << endl; Point shiftPt = phaseCorrelate(grayL64F, grayR64F);
cout << shiftPt << endl; 待拼接左圖向左平移205pixel,向下平移60pixel與待拼接右圖左上角重合,[-205, 60]即為水準和豎直方向的平移量。
完整代碼與拼接結果:
// 06_Image_Stitch_PhaseCorrelate.cpp : 此檔案包含 "main" 函數。程式執行将在此處開始并結束。
// 公衆号:OpenCV與AI深度學習
// 環境 VS2017 + OpenCV4.4.0
// 功能介紹:基于相位相關的圖像拼接
#include "pch.h"
#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main()
{
Mat imgL = imread("./imgs/01.jpg");
Mat imgR = imread("./imgs/02.jpg");
double start = getTickCount();
Mat grayL, grayR;
cvtColor(imgL, grayL, COLOR_BGR2GRAY);
cvtColor(imgR, grayR, COLOR_BGR2GRAY);
Mat grayL64F, grayR64F;
grayL.convertTo(grayL64F, CV_64F);
grayR.convertTo(grayR64F, CV_64F);
Point shiftPt = phaseCorrelate(grayL64F, grayR64F);
cout << shiftPt << endl;
Mat dstImg(imgL.rows, imgR.cols + abs(shiftPt.x), CV_8UC3, Scalar::all(0));
Mat roiLeft = dstImg(Rect(0, 0, imgL.cols, imgL.rows));
imgL.copyTo(roiLeft);
Mat roiRight = dstImg(Rect(-shiftPt.x, 0, imgR.cols, imgR.rows - shiftPt.y));
Mat cutImg = imgR(Rect(0, shiftPt.y, imgR.cols, imgR.rows - shiftPt.y));
cutImg.copyTo(roiRight);
Mat debugImg = dstImg.clone();
rectangle(debugImg, Point(-shiftPt.x, -shiftPt.y), Point(dstImg.cols-1, imgR.rows - shiftPt.y), Scalar(0, 255, 0), 2, 8);
imwrite("match.jpg", debugImg);
double end = getTickCount();
double useTime = (end - start) / getTickFrequency();
cout << "use-time : " << useTime << "s" << endl;
imwrite("dst.jpg", dstImg);
cout << "Done!" << endl;
return 0;
} 拼接結果圖:
比對區域:
結尾語
[1] 相位相關法相比模闆比對方法可以自動計算偏移量,省去設定模闆的步驟;
[2] 在特征點較少的圖像拼接情況下,特征比對如SIFT/SURF可能會失敗,此時可嘗試相位相關法:
[3] 相位相關法不适用圖像有周期性重複區域的圖像,如棋盤格圖像。
[4] 上面代碼隻給出了一種左右拼接情形,實際應用需根據水準和豎直方向平移量正負判斷拼接方向和位置。
[5] 一些畸變明顯的圖像不能單純靠此方法得到好的效果。