在4.0.1節中,我們已經介紹了一個簡單的圖像形成模型,即照射-反射模型。這個模型可以開發一種頻率處理程式,該程式可以同時壓縮灰階範圍和增強對比度來改善一幅圖像的表現。圖像形成的照射-反射模型的表達式如下:
f(x,y)=i(x,y)r(x,y) 6.4- 16
上式不能直接用于對照射和反射的頻率分量進行操作,因為兩個分量的傅裡葉變換之積,不等于原圖像的傅裡葉變換:
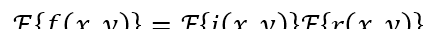
6.4- 17
但是,我們可以定義如下變換關系:
6.4- 18
然後再對上式兩邊做傅裡葉變換:
6.4- 19
得到下面的傅裡葉變換域的等式:
6.4- 20
其中, 分别是 的傅裡葉變換。
我們可以用一個濾波器 對 濾波,故有:
6.4- 21
在空間域中,濾波後的圖像為:
6.4- 22
我們可以将上式改寫成簡略形式:
6.4- 23
其中,
6.4- 24
6.4- 25
最後,因為 是通過取輸入圖像的自然對數形成的,我們可通過取濾波後的結果的指數這一反處理來形成輸出圖像:
6.4- 26
6.4- 27
6.4- 28
經濾波處理後的照射和反射分量。
以上推到的濾波方法流程圖,如圖6. 26所示。該濾波方法是針對特定成像系統,在此稱為同态系統。在這種特殊應用中,方法的關鍵在于照射分量和反射分量的分離,其實作形式(6.4-20)所示。然後,如式(6.4-21)那樣,用同态濾波器 對這些分量進行濾波操作。
圖像的照射分量通常由慢的空間變化來表征,而反射分量往往引起突變,特别是在不同物體的連接配接部分。這些特性導緻圖像取對數後的傅裡葉變換的低頻成分與照射分量相聯系,而高頻成分與反射分量相聯系。雖然這些聯系隻是粗略的近似,但它們用在圖像濾波中是有益的。
圖6. 27所示的函數形狀可用高通濾波器的基本形式來近似。例如,采用形式稍微變化一下的高斯高通濾波器可得到函數:使用同态濾波器可更好地控制照射分量和反射分量。這種控制需要指定一個濾波器函數 ,它可用不同的可控方法影響傅裡葉變換的低頻和高頻分量。圖6. 27顯示了這種濾波器的剖面圖。如果 和 標明, 且 ,那麼圖6. 27所示濾波器函數趨向于衰減低頻(照射)的貢獻。
6.4- 29
其中 由式(6.3-2)定義,常數c控制函數坡度的銳利度,它在 和 之間過渡。這個濾波器類似于前面6.4.3節讨論的高頻強調濾波器。
例6. 10 使用同态濾波增強圖像
圖6. 28(a)顯示了一幅大小為1162×746像素的全身PET掃描圖像。圖像稍微有些模糊,并且由于主導顯示動态範圍的高灰階“熱點”使得其許多低灰階特征很朦胧(這些“熱點”是由腦部的惡性良性腫瘤和肺部的惡性良性腫瘤導緻的)。
圖6. 28(b)是圖6. 28(a)經同态濾波湖得到的結果,使用式(6.4-8)中的濾波器, 。改濾波器的剖面看上去正好像圖6. 27,隻是坡度有點陡峭。
下面是主程式:Mat homoMorphicFilter(const Mat& src,double D0,
double gammaH,double gammaL,double c)
{
int rows=src.rows,cols=src.cols,channels=src.channels();
Mat srcLog,src64d;
src.convertTo(src64d,CV_64FC1);
cv::log(src64d+1,srcLog);
Mat srcLogFft=fft(srcLog);
dftshift(srcLogFft);
//建立同态濾波器
Mat Huv(rows,cols,CV_64FC2,Scalar::all(0));//頻域濾波器
int cx=cols/2,cy=rows/2;
double D2=D0*D0;
for(int i=0;i<rows;i++)
{
Vec2d* p=Huv.ptr<Vec2d>(i);
for(int j=0;j<cols;j++)
{
double x=j-cx,y=i-cy;
p[j][0]=(gammaH-gammaL)*(1-c*exp(-(x*x+y*y)/D2))+gammaL;
p[j][1]=p[j][0];
}
}
Huv /=(rows*cols);
//頻域濾波,在頻域與Huv逐點相乘
Mat ftProduct=srcLogFft.mul(Huv);
//逆傅裡葉變換
Mat ftInv=fft(ftProduct,DFT_INVERSE);
//計算逆傅裡葉變換的幅值
Mat mag= myMagnitude(ftInv);
Mat edst;
cv::exp(mag,edst);
normalize(edst,edst,255,0,NORM_MINMAX);
edst.convertTo(edst,CV_8UC1);
return edst;
} int main()
{
Mat img=imread("D:/CodeWork/MyImage/Fig0462a.tif",0);
imshow("rogin img",img);
Mat imgHomo=homoMorphicFilter(img,80,3,0.25,1.);
imshow("homoMorphic filter",(imgHomo+img)/2);
waitKey();
return 0;
}
下面左圖是經過同态濾波後的結果,右圖是原圖像:
例6.9中的胸部透視圖像的同态濾波:
int main()
{
Mat img=imread("D:/CodeWork/MyImage/Fig0459a.tif",0);
imshow("rogin img",img);
Mat imgHomo=homoMorphicFilter(img,60,2,0.25,1.);
imgHomo =imgHomo*0.5+img*0.5;
equalizeHist(imgHomo,imgHomo);
imshow("homoMorphic filter",imgHomo);
waitKey();
return 0;
} 下面是胸部透視圖像,左邊是原圖,右邊是同态濾波的結果:
轉載于:https://www.cnblogs.com/phoenixdsg/p/8414277.html