T1、傾斜的線
平面上給定 \(n \ (n \leq 10 ^ 5)\) 個整點,選兩個點使經過他們的直線斜率在數值上最接近 \(\frac{P}{Q} \ (1 \leq P,Q \leq 10 ^ 9)\);
以最簡分數形式輸出這個斜率,保證答案大于 \(0\),且不會有橫坐标或縱坐标相等的點。
\(Sol\):
過每個點作一條斜率為 \(\frac{P}{Q}\) 的直線,把點按照直線的截距排序;
對于排序後的點,不難證明一個點的最優答案一定是它和與它相鄰的某個點所在的直線。
時間複雜度 \(O(n \log_2 n)\)。
這道題好像不太能用整數做,直接 \(long \ double\) 即可。
\(Source\):
//#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <algorithm>
#include <cmath>
typedef long double db;
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 2e5 + 5;
const db eps = 1e-15;
struct node {
int x, y;
} a[N];
int n, P, Q;
inline bool cmp(const node &i, const node &j) {
return 1ll * P * i.x - 1ll * Q * i.y < 1ll * P * j.x - 1ll * Q * j.y;
}
int gcd(int _, int __) {
return __ ? gcd(__, _ % __) : _;
}
int main() {
//freopen("in", "r", stdin);
freopen("slope.in", "r", stdin);
freopen("slope.out", "w", stdout);
n = in(), P = in(), Q = in();
int d = gcd(P, Q); P /= d, Q /= d;
for (int i = 1; i <= n; ++i)
a[i].x = in(), a[i].y = in();
std::sort(a + 1, a + 1 + n, cmp);
int ansx = 1, ansy = 2;
db min = (db)(a[1].y - a[2].y) / (db)(a[1].x - a[2].x), base = (db)P / Q, M;
for (int i = 3; i <= n; ++i) {
M = (db)(a[i].y - a[i - 1].y) / (db)(a[i].x - a[i - 1].x);
if (fabs(fabs(M - base) - fabs(min - base)) < eps) {
if (M - base < eps)
ansx = i - 1, ansy = i;
} else if (fabs(M - base) - fabs(min - base) < eps) {
min = M, ansx = i - 1, ansy = i;
}
}
d = gcd(std::abs(a[ansx].y - a[ansy].y), std::abs(a[ansx].x - a[ansy].x));
printf("%d/%d\n", std::abs(a[ansx].y - a[ansy].y) / d, std::abs(a[ansx].x - a[ansy].x) / d);
return 0;
} T2、最小值
給定一個長度為 \(n \ (n \leq 2 \times 10 ^ 5)\) 的整數序列 \(a\)。
定義一個區間 \([l,r]\) 的價值為 \(f( \min_{i = l} ^ {r} a_i )\), 其中: \(f(x) = Ax ^ 3 + B x ^ 2 + C x + D\)。
把序列 \(a\) 劃分成若幹區間,求最大價值和。
\(|f(x)| \leq 10 ^ {13}\),輸入資料在 \(int\) 以内。
\(Sol\):
記 \(dp_i\) 表示序列前 \(i\) 位劃分出的最大價值,顯然有:
\[ dp_i = \max_{j = 0} ^ {i - 1} \{ dp_j + f( min[j + 1,i] ) \} \]
單調棧優化即可。
時間複雜度 \(O(n)\)。
\(Source\):
#include <cstdio>
#include <cstring>
#include <algorithm>
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 2e5 + 5;
int n, a[N], A, B, C, D;
std::pair<int, long long> sta[N];
int tp;
long long dp[N];
inline long long f(const int x) {
return 1ll * x * (1ll * x * (1ll * x * A + B) + C) + D;
}
int main() {
//freopen("in", "r", stdin);
freopen("min.in", "r", stdin);
freopen("min.out", "w", stdout);
n = in(), A = in(), B = in(), C = in(), D = in();
for (int i = 1; i <= n; ++i)
a[i] = in();
dp[0] = 0;
long long tmp;
for (int i = 1; i <= n; ++i) {
tmp = dp[i - 1];
while (tp && a[sta[tp].first] >= a[i])
chk_max(tmp, sta[tp--].second);
dp[i] = tmp + f(a[i]);
if (tp)
chk_max(dp[i], dp[sta[tp].first]);
sta[++tp] = std::make_pair(i, tmp);
}
printf("%lld\n", dp[n]);
return 0;
} T3、安排
給定兩個長度為 \(n \ (n \leq 2 ^ {12})\) 的排列 \(A,B\),現需通過以下操作将 \(A\) 變成 \(B\):
選擇一個區間 \([l,r]\),交換這個區間裡最大和最小的元素。
操作次數不能超過 \(345678\),輸出一種方案。
\(Sol\):
老虎蒜頭神仙題。
這個操作十分的不可控,要盡量讓它可控,我們隻能對一個有序區間進行操作。
不難發現,該操作 (交換) 是可逆的,是以可以将 \(A,B\) 分别排序,再按實際操作順序輸出。
排序的話,堆排、快排等算法顯然不好用,考慮歸并。
歸并的關鍵在于如何合并兩個排好序的區間,這裡用到了快排的思想,如下圖;
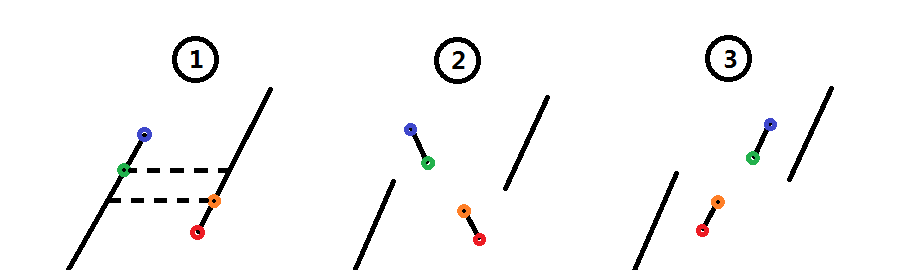
這樣可以把兩個區間分成兩個新的部分,并且右邊一定比左邊大,遞歸即可。
這樣合并一次的複雜度是 \(O(n \log_2 n)\)。
根據主定理,有 \(T(n) = 2T( \frac{n}{2} ) + n \log_2n = n \log_2 ^ 2 n\),總複雜度 \(O(n \log_2^2 n)\)。
我合并時寫了随機化 (逃);
由于一些不可描述的邊界問題,我也不知道這份代碼對不對 (但它過了),歡迎 \(hack\)。
\(Source\):
//#pragma GCC optimize(3,"Ofast","inline")
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstdlib>
int in() {
int x = 0; char c = getchar(); bool f = 0;
while (c < '0' || c > '9')
f |= c == '-', c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return f ? -x : x;
}
template<typename T>inline void chk_min(T &_, T __) { _ = _ < __ ? _ : __; }
template<typename T>inline void chk_max(T &_, T __) { _ = _ > __ ? _ : __; }
const int N = 1e4 + 5;
int n, a[N], b[N];
std::vector<std::pair<int, int> > opt[2];
inline void swap(int &x, int &y) {
int t = x; x = y, y = t;
}
void rever(int l, int r, int k, int *f) {
while (l < r) {
swap(f[l], f[r]);
opt[k].push_back(std::make_pair(l++, r--));
}
}
void quick_merge(int l, int mid, int r, int k, int *f) {
if (l >= r)
return ;
if (l + 1 == r) {
if (f[l] > f[r])
rever(l, r, k, f);
return ;
}
if (f[mid] < f[mid + 1])
return ;
if (f[l] > f[r]) {
rever(l, mid, k, f);
rever(mid + 1, r, k, f);
rever(l, r, k, f);
return ;
}
int p1 = std::upper_bound(f + l, f + mid + 1, f[mid + 1]) - f;
int p2 = std::upper_bound(f + mid + 1, f + r + 1, f[mid]) - f - 1;
int p3, p4;
if (mid - p1 + 1 < p2 - mid) {
if (r - mid <= 1000) {
p4 = (mid + 1 + p2) >> 1;
} else {
p4 = rand() % (p2 - mid) + mid + 1;
}
p3 = std::upper_bound(f + p1, f + mid + 1, f[p4]) - f;
} else {
if (mid - p1 + 1 <= 1000) {
p3 = (p1 + mid) >> 1;
} else {
p3 = rand() % (mid - p1 + 1) + p1;
}
p4 = std::upper_bound(f + mid + 1, f + p2 + 1, f[p3]) - f - 1;
}
rever(p3, mid, k, f);
rever(mid + 1, p4, k, f);
rever(p3, p4, k, f);
quick_merge(l, p3 - 1, p3 - 1 + p4 - mid, k, f);
quick_merge(p4 - (mid - p3), p4, r, k, f);
}
void merge_sort(int l, int r, int k, int *f) {
if (l == r)
return ;
int mid = (l + r) >> 1;
merge_sort(l, mid, k, f), merge_sort(mid + 1, r, k, f);
quick_merge(l, mid, r, k, f);
//for (int i = 1; i <= n; ++i)
// printf("%d ", f[i]);
//puts("");
}
int main() {
//freopen("in", "r", stdin);
freopen("swap.in", "r", stdin);
freopen("swap.out", "w", stdout);
srand(40051326);
n = in();
for (int i = 1; i <= n; ++i)
a[i] = in();
for (int i = 1; i <= n; ++i)
b[i] = in();
merge_sort(1, n, 0, a);
merge_sort(1, n, 1, b);
printf("%d\n", (int)(opt[0].size() + opt[1].size()));
for (unsigned i = 0; i < opt[0].size(); ++i)
printf("%d %d\n", opt[0][i].first, opt[0][i].second);
std::reverse(opt[1].begin(), opt[1].end());
for (unsigned i = 0; i < opt[1].size(); ++i)
printf("%d %d\n", opt[1][i].first, opt[1][i].second);
return 0;
} 轉載于:https://www.cnblogs.com/15owzLy1-yiylcy/p/11370552.html