全解題報告索引目錄 -> 【北大ACM – POJ試題分類】
轉載請注明出處:http://exp-blog.com
-------------------------------------------------------------------------
大緻題意:
一個1X1的正方形,每條邊上有n個不同的點(不包括頂點),并給出它們的坐标。現在把對邊相對應的點相連,将正方形分割成(n+1)*(n+1)個小四邊形。問最大的四邊形的面積是多少。
解題思路:
計算幾何求面積的題,算半條水題吧。。
基本思路:
構造所有的線段,然後枚舉每對水準-豎直線段,求交點,然後計算四邊形面積,求最大值。
應用知識:
叉積(規範相交)
多邊形分解
三角形基于計算幾何的面積公式(注意正負)
我先建立一個數學模型說明問題:
以n=3為例畫圖 (當然實際上内部的線不一定是正交的,這裡隻是為了簡單說明)
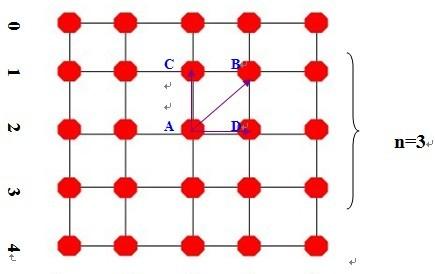
第一步建立一個大小為 (n+2)*(n+2) 的二維交點矩陣node,每個元素存儲一個交點坐标(x,y)
由于四角交點為定點,每條邊上的交點又是輸入值,那麼外圍一圈的交點都是已知了
由于對邊的點是對應相連的,是以要求的就是内部n*n個交點
顯然地,所求的所有交點都是某兩條直線規範相交所得,是以就可以直接使用求規範相交的交點的公式,而不需要套用模闆了
交點公式 (及推導過程) 請參看 劉汝佳《算法藝術與資訊學競賽》P357 這裡不再說明
通過兩兩枚舉所有内部直線,就能得到 交點矩陣node[][]
那麼剩下的問題就是求出所有 簡單四邊形(不包含其他四邊形) 的面積,輸出最大的一個。那麼問題就是:已知一個不規則四邊形四個角的坐标,求它的面積
由于四邊形是不規則的,直接求解其面積是非常困難的,唯有将其劃分為兩個三角形,分别求出兩個三角形的面積,再相加
如圖,我求解所有四邊形時都是采用如圖的劃分方法
那麼問題進一步轉化為“已知不規則三角形三個角的坐标,如何求其面積”
不用比較都看得出,計算幾何的方法遠遠優于解析幾何,不但省去計算一堆長度的麻煩(避免了精度誤差),而且還能利用計算交點時 計算叉積的功能函數cross()
使用計算幾何,不但運算量大大減少了,代碼也寫少了,結果還更精确
不過有一點要注意的是,計算幾何計算的面積是有方向的,即面積可能為負,是以絕對值必不可少,這點千萬注意
//Memory Time
//544K 16MS
#include<iostream>
#include<cmath>
#include<iomanip>
using namespace std;
typedef class Node
{
public:
double x,y;
}location;
double det(double x1,double y1,double x2,double y2)
{
return x1*y2-x2*y1;
}
double cross(location A,location B,location C,location D) //計算 AB x CD
{
return det(B.x-A.x , B.y-A.y , D.x-C.x , D.y-C.y);
}
/*Compute Intersection*/
double xx,yy; //坐标傳回值
void intersection(location A,location B,location C,location D)
{
double area1=cross(A,B,A,C);
double area2=cross(A,B,A,D);
xx=(area2*C.x - area1*D.x)/(area2-area1); //本題所求的交點一定是規範相交所得,是以無需判斷是否規範相交
yy=(area2*C.y - area1*D.y)/(area2-area1);
return;
}
/*Compute Area*/
double area(location A,location B,location C,location D)
{
double triangle1=fabs(0.5*cross(A,B,A,C)); //用計算幾何的方法計算的面積是有向面積
double triangle2=fabs(0.5*cross(A,B,A,D)); //即算出來的面積可能為負數,是以必須用絕對值
// fabs() 為取double的絕對值函數
return triangle1+triangle2;
}
int main(int i,int j,int k)
{
int n;
while(cin>>n)
{
if(!n)
break;
/*Initial*/
location** node=new location*[n+2];
node[0]=new location[n+2]; //下邊
node[n+1]=new location[n+2]; //上邊
/*Input Down-edge*/
node[0][0].x = node[0][0].y =0.0;
for(i=1;i<=n;i++)
{
cin>>node[0][i].x;
node[0][i].y=0.0;
}
node[0][n+1].x=1.0;
node[0][n+1].y=0.0;
/*Input Up-edge*/
node[n+1][0].x=0.0;
node[n+1][0].y=1.0;
for(i=1;i<=n;i++)
{
cin>>node[n+1][i].x;
node[n+1][i].y=1.0;
}
node[n+1][n+1].x=1.0;
node[n+1][n+1].y=1.0;
/*Input Left-edge*/
for(i=1;i<=n;i++)
{
node[i]=new location[n+2];
cin>>node[i][0].y;
node[i][0].x=0.0;
}
/*Input right-edge*/
for(i=1;i<=n;i++)
{
cin>>node[i][n+1].y;
node[i][n+1].x=1.0;
}
/*Compute Intersection*/
for(j=1;j<=n;j++)
for(i=1;i<=n;i++)
{
intersection(node[0][j],node[n+1][j],node[i][0],node[i][n+1]);
node[i][j].x=xx;
node[i][j].y=yy;
}
/*Compute Area*/
double max_area=0.0;
for(i=1;i<=n+1;i++)
for(j=1;j<=n+1;j++)
{
double temp=area(node[i-1][j-1],node[i][j],node[i][j-1],node[i-1][j]);
if(max_area < temp)
max_area = temp;
}
/*Output*/
cout<<fixed<<setprecision(6)<<max_area<<endl;
/*Realx Room*/
delete[] node;
}
return 0;
}