題意:求嚴格的次小生成樹
嚴格次小生成樹:(value(e)表示邊e的權值) ∑e∈EM value(e)<∑e∈ES value(e)(EM為最小生成樹邊集,ES為次小生成樹邊集)
就是次小生成樹邊權和一定要小于最小生成樹, 而非嚴格的就不一定,也可能等于。
非嚴格次小生成樹求法:是在最小生成樹邊集外 找到一條邊(假設兩點為u,v)(一定大于等于最小生成樹裡的邊),替換掉最小生成樹中u,v之間最大邊,使得兩者內插補點最小。 主要是要儲存最小生成樹兩點之間最大邊。
嚴格次小生成樹與非嚴格相似,但是要儲存兩點之間 最大邊和次大邊, 因為最小生成樹邊集外 的邊等于最大邊時,代替次大邊否則就是代替最大邊。 而這裡用到了lca最近公共祖先,為了保證聯通
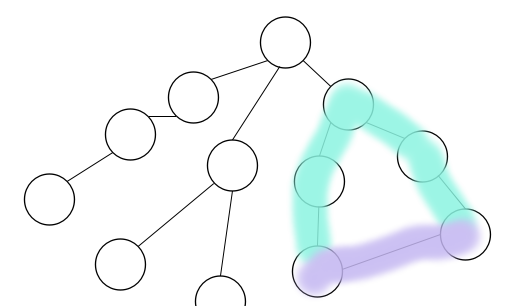
如圖:假設除去紫色的邊是 最小生成樹, 我們的目标是用紫色的邊代替 環中的小于紫邊最大的邊。
是以這裡用到了lca,假設紫邊兩點為u,v, 先找到u,v的最近公共祖先點 fa,就分兩邊 找u,fa之間的最大小于紫邊的邊 和v,fa之間最大小于紫邊的邊
這樣周遊每條不在最小生成樹中的邊,找到最小的 紫邊與代替邊的內插補點,加上最小生成樹邊權和就是答案。
最後我們來總結下步驟:
第一步:用kruskal 找到最小生成樹,記算邊權和,和 标記最小生成樹中的邊。
第二步:dfs搜尋 記錄最小生成樹中兩點的最近公共祖先, 并用同樣的方式記錄 兩點之間最大邊和最次邊。
第三步:枚舉不在最小生成樹中的邊,lca找到邊兩點的最近公共祖先,分兩邊查找最大小于這條邊的邊權值。
最後:找到最小的內插補點加上最小生成樹邊權和即可。
代碼中一直貫徹着倍增的思想。詳細可以看代碼:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
const int maxm=3e5+100;
struct node{
int u,v,w,nxt;
}e[2*maxm];
struct edge{
int x,y,z,tag;
}ee[maxm];
int head[maxn],bz[maxn][22];//bz[i][j]記錄i的2^j祖先
int maxi[maxn][22],mini[maxn][22],lg[maxn];
//maxi[i][j],記錄i到2^j祖先之間的最大邊權值,mini是記錄次邊值
//lg[i]表示log_2(i)+1,用來優化lca的,可以不用
int depth[maxn],fa[maxn],n,m,cnt;
bool cmp(edge a,edge b)
{
return a.z<b.z;
}
void add(int u,int v,int w)
{
e[cnt].u=u;
e[cnt].v=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt++;
}
void dfs(int f,int fath)//記錄最小生成樹中兩點之間的最近公共祖先和最大邊,次大邊
{
bz[f][0]=fath;
depth[f]=depth[fath]+1;
for(int i=1;(1<<i)<=depth[f];i++)
{
bz[f][i]=bz[bz[f][i-1]][i-1];//lca中的核心轉換
mini[f][i]=max(mini[f][i-1],mini[bz[f][i-1]][i-1]);
maxi[f][i]=max(maxi[f][i-1],maxi[bz[f][i-1]][i-1]);
if(maxi[f][i-1]!=maxi[bz[f][i-1]][i-1])
mini[f][i]=max(mini[f][i],min(maxi[f][i-1],maxi[bz[f][i-1]][i-1]));
}
for(int i=head[f];i!=-1;i=e[i].nxt)
{
if(e[i].v!=fath)
{
maxi[e[i].v][0]=e[i].w;
mini[e[i].v][0]=-1;
dfs(e[i].v,f);
}
}
}
int lca(int x,int y)//lca求最近公共祖先
{
if(depth[x]<depth[y])//使x深度大于y
swap(x,y);
while(depth[x]>depth[y])//跳到相同深度
x=bz[x][lg[depth[x]-depth[y]]-1];
if(x==y)
return x;
for(int k=lg[depth[x]]-1;k>=0;k--)//往上找,直到x,y跳到最近公共祖先的下一節點
if(bz[x][k]!=bz[y][k])
x=bz[x][k],y=bz[y][k];
return bz[x][0];//傳回最近公共祖先
}
int find(int x)
{
return fa[x]==x?x:fa[x]=find(fa[x]);
}
int qmax(int u,int v,int w)//找到u,v之間小于 w大最大邊
{
int ans=-inf;
for(int i=lg[depth[u]]-1;i>=0;i--)
{
if(depth[bz[u][i]]>=depth[v])
{
if(w!=maxi[u][i])//不等于最大邊,取最大邊
ans=max(ans,maxi[u][i]);
else//等于,取次大邊
ans=max(ans,mini[u][i]);
u=bz[u][i];//往上跳
}
}
return ans;
}
int main()
{
cnt=0;
ll sum=0;
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
fa[i]=i;
for(int i=1;i<=n;i++)//lca常數優化,lg[i]表示log_2(i)+1;
lg[i]=lg[i-1]+(1<<lg[i-1]==i);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&ee[i].x,&ee[i].y,&ee[i].z);
sort(ee+1,ee+m+1,cmp);
for(int i=1;i<=m;i++)//kruskal
{
int fx=find(ee[i].x);
int fy=find(ee[i].y);
if(fx!=fy)
{
sum+=ee[i].z;
ee[i].tag=1;
fa[fx]=fy;
add(ee[i].x,ee[i].y,ee[i].z);
add(ee[i].y,ee[i].x,ee[i].z);
}
}
dfs(1,0);
int ans=inf;
for(int i=1;i<=m;i++)//枚舉不在最小生成樹的邊
{
if(!ee[i].tag)
{
int lc=lca(ee[i].x,ee[i].y);
int res=max(qmax(ee[i].x,lc,ee[i].z),qmax(ee[i].y,lc,ee[i].z));
ans=min(ans,ee[i].z-res);//ans尋找最小內插補點
}
}
printf("%lld\n",sum+ans);//答案就是最小生成樹邊權和加最小內插補點
return 0;
} 轉載于:https://www.cnblogs.com/xiongtao/p/11162539.html