- 峰度(Kurtosis)
- 定義
峰度又稱峰态系數,表征機率密度分布曲線在平均值處峰值高低的特征數,即是描述總體中所有取值分布形态陡緩程度的統計量。直覺看來,峰度反映了峰部的尖度。這個統計量需要與正态分布相比較。
-
- 公式
定義上峰度是樣本的标準四階中心矩(standardized 4rd central moment)。
随機變量的峰度計算方法為随機變量的四階中心矩與方差平方的比值。
具體計算公式為:
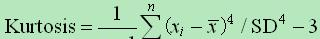
-
- 性質
峰度為0表示該總體資料分布與正态分布的陡緩程度相同;
峰度 >0表示該總體資料分布與正态分布相比較為陡峭,為尖頂峰;
峰度 <0表示該總體資料分布與正态分布相比較為平坦,為平頂峰。
峰度的絕對值數值越大表示其分布形态的陡緩程度與正态分布的差異程度越大。
- 偏度(Skewness)
- 定義
偏度與峰度類似,它也是描述資料分布形态的統計量,其描述的是某總體取值分布的對稱性的特征統計量。
-
- 公式
定義上偏度是樣本的标準三階中心矩(standardized 3rd central moment)。
偏度的具體計算公式為:
-
- 性質
這個統計量同樣需要與正态分布相比較,
偏度為0表示其資料分布形态與正态分布的偏斜程度相同;
偏度 >0表示其資料分布形态與正态分布相比為正偏或右偏,即有一條長尾巴拖在右邊,資料右端有較多的極端值,資料均值右側的離散程度強;
偏度 <0表示其資料分布形态與正态分布相比為負偏或左偏,即有一條長尾拖在左邊,資料左端有較多的極端值,資料均值左側的離散程度強
偏度的絕對值數值越大表示其分布形态的偏斜程度越大。
轉載于:https://www.cnblogs.com/zwt20120701/p/10872243.html