首先來幾個部落格:
1、https://www.jianshu.com/p/c57ef1508fa7
2、http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
3、https://blog.csdn.net/lvhao92/article/details/50805021
4、https://blog.csdn.net/zouxy09/article/details/8537620
複述:
1、EM算法第一印象:
a、它是種特别的極大似然估計。
b、它的特殊性在于含有隐變量。
c、它是一種算法不是模型,使用該算法的模型,屬于生成模型。
回想下似然函數=>邏輯回歸=>李航的書79頁=>P(Y=1|x)=π(x),P(Y=0|x)=1-π(x)=>P就是參數,y就是觀測到的變量=>已經觀測到了一系列的y值,最大似然就是求參數P,使得組成目前這一系列y的機率最大。
可以看到,y是可觀測的序列,然鵝現實世界是複雜的,在你看到的表象的背後,還有陰暗的東西,冥冥之中操縱着y,但是我們看不到那個隐藏的東西,EM算法就是将隐變量及其對應的參數都最大似然出來。
如果還是不了解到底隐藏變量是啥,那麼舉個栗子(依然抛硬币)吧:
現在有兩個硬币A和B,要估計的參數是它們各自翻正面(head)的機率。為什麼是硬币A和B兩個硬币呢?說明A和B應該是不同的,因為我們還有個隐藏的變量C,我們要以C的取值來決定抛A還是B,但是我們列不出來C的序列(它是隐藏的,觀測不到)。我們隻有一系列硬币正面和反面的資料,比如硬币被抛了10次,我們記錄下來的隻有H T T T H H T H T H,這麼一個序列,至于序列裡面哪些是A得到的T和H,哪些是B得到的T和H,我們不知道。但是我們可以用EM來估計出A出現的機率、B出現的機率,它們倆的出現的機率就是變量C對應的參數,我們還可以用EM來估計出A是正反面的機率也就是變量A的參數,B是正反面的機率也就是B的參數。
下面這個例子是真的好:
現在有兩個硬币A和B,要估計的參數是它們各自翻正面(head)的機率。觀察的過程是先随機選A或者B,然後扔10次。以上步驟重複5次。
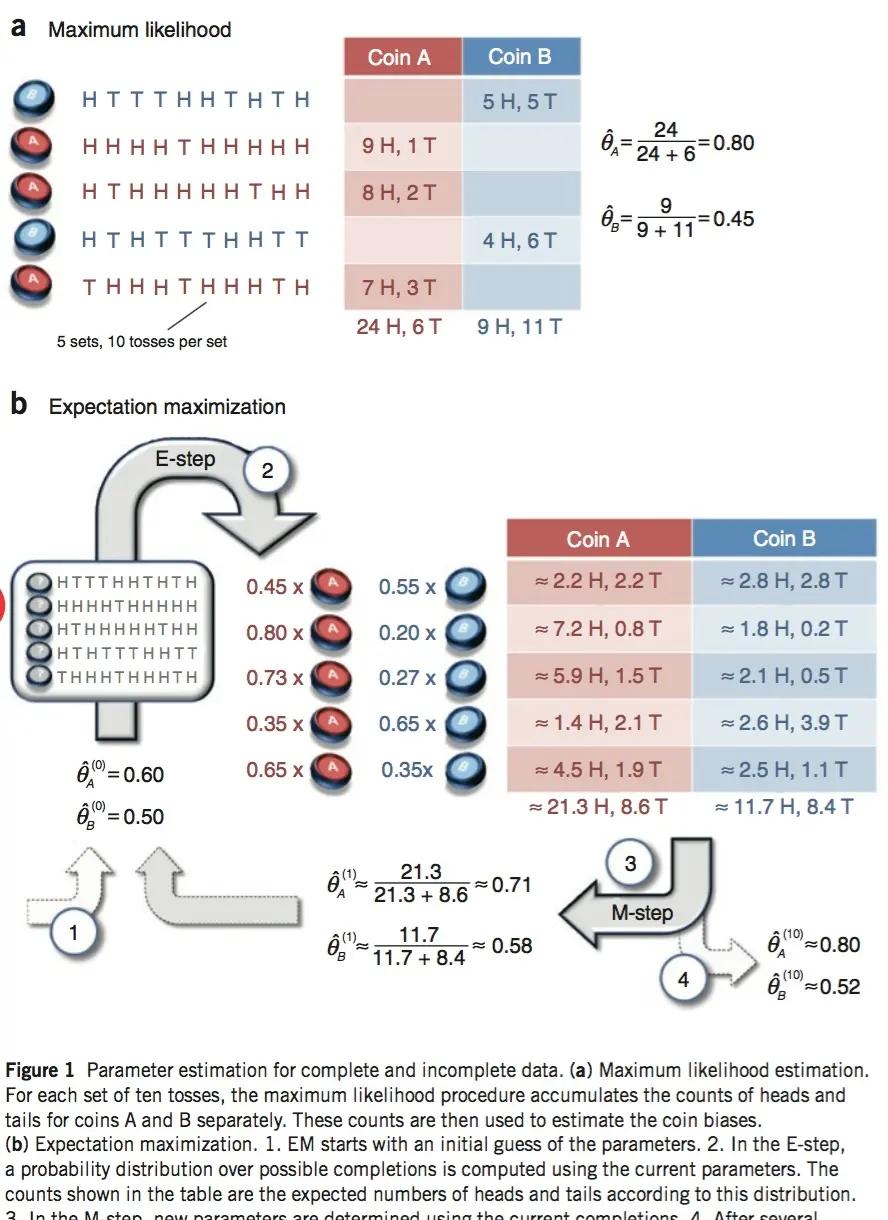
下圖是别人給的解釋:
由圖我們知道:
對于因變量C,我們不知道它的取值序列,但是我們應該得知道它的取值範圍,或者可取哪些值,在該例子中,也就是我們得知道隐變量C的值有A和B兩種。
對上面第二個圖的解釋:
按照EM算法的思想:
a、我們先假定(或者說給初始值)A正面朝上的機率為0.6,即:,B正面朝上的機率為0.5,但是我們不給隐變量C為A和為B的機率(可能因為它是隐變量,對它比較歧視吧)。
b、我們有了觀測序列,也就是HHHHTHHHHH,我們可以求出該觀測序列來自A的機率和來自B的機率,具體的做法就是:
假設隻使用硬币A抛出上面的結果,記為P(A),那麼:
,假設隻使用硬币B抛出上面的結果,記為P(B),那麼
,當然,觀測序列的取值很有可能是有的是抛A得到的,有的是抛B得到的,那麼在P(A)及P(B)已知的情況下,通過
,就可以知道序列裡抛A的機率,也就知道了抛B的機率,也就是序列來自A的機率及序列來自B的機率。我們已經看到觀測序列的結果為9個H和1個T,那麼來自A的H的個數就是0.8*9=7.2個,來自A的T的個數就是0.8個,來自B的H的個數就是0.2*9=1.8個,來自B的T的個數就是0.2*1=0.2個。
c、我們可以擷取多個觀測序列,這些觀測序列都按照a-b的步驟計算:來自A的H的個數,來自A的T的個數,來自B的H的個數,來自B的T的個數(比如上圖b),然後對來自A的H和T進行統計,可以計算得到新的,抛A得到H和T的機率,及抛B得到H和T的機率:
然重複b-c,最終重複10次,我們得到了最優解:
,即A正面的機率及B正面的機率,其實我們也得到了來自A和來自B的機率,但是這個機率是因變量的參數。
一些總結:
EM算法的輸出就是參數θ,θ對應的變量既包含隐變量也包含已知變量。
怎麼能對EM有個簡單的認識:
回顧邏輯回歸中似然函數的形式: