07年NOIp模拟賽by Matrix67 解題報告

Problem 1: Matrix67的情書（二）

    大家都知道，看一個數是否能被2整除隻需要看它的個位能否被2整除即可。可是你想過為什麼嗎？這是因為10能被2整除，是以一個數10a+b能被2整除當且僅當b能被2整除。大家也知道，看一個數能否被3整除隻需要看各位數之和是否能被3整除。這又是為什麼呢？答案或多或少有些類似：因為10^n-1總能被3整除。2345可以寫成2*(999+1) + 3*(99+1) + 4*(9+1) + 5，展開就是2*999+3*99+4*9 + 2+3+4+5。前面帶了數字9的項肯定都能被3整除了，于是要看2345能否被3整除就隻需要看2+3+4+5能否被3整除了。當然，這種技巧隻能在10進制下使用，不過類似的結論可以推廣到任意進制。

    注意到36是4的整數倍，而ZZZ...ZZ除以7總是得555...55。也就是說，判斷一個36進制數能否被4整除隻需要看它的個位，而一個36進制數能被7整除當且僅當各位數之和能被7整除。如果一個數同時能被4和7整除，那麼這個數就一定能被28整除。于是問題轉化為，有多少個連續句子滿足各位數字和是7的倍數，同時最後一個數是4的倍數。這樣，我們得到了一個O(n)的算法：用P[i]表示前若幹個句子除以7的餘數為i有多少種情況，掃描整篇文章并不斷更新P數組。當某句話的最後一個字能被4整除時，假設以這句話結尾的字首和除以7餘x，則将此時P[x]的值累加到最後的輸出結果中（兩個字首的數字和除以7餘數相同，則較長的字首多出來的部分一定整除7）。

    上述算法是我出這道題的本意，但比賽後我見到了其它各種各樣新奇的算法。比如有人注意到36^n mod 28總是等于8，利用這個性質也可以構造出類似的線性算法來。還有人用動态規劃（或者說遞推）完美地解決了這個問題。我們用f[i,j]表示以句子i結束，除以28餘數為j的文本片段有多少個；處理下一句話時我們需要對每一個不同的j進行一次掃描，把f[i-1,j]加進對應的f[i,j']中。最後輸出所有的f[i,0]的總和即可。這個動态規劃可以用滾動數組，是以它的空間同前面的算法一樣也是常數的。

    如果你完全不知道我在說什麼，你可以看看和進位制、同餘相關的文章。另外，我之前還曾出過一道很類似的題(VOJ1090)，你可以對比着看一看。

    另外，非常抱歉地告訴大家，這道題的最後一個資料是錯的。這個資料的第一個句子是一個空句子（感謝Ai.Freedom的提醒）。很多第一題隻得了90分的好同志估計都是由于我的失誤造成的，這裡再次表示歉意。如果去掉最前面的那個問号，輸出應該是19511110。

Problem 2: 送給MM的生日禮物

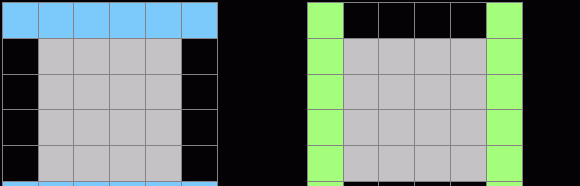
    我們用f[i,j,k]表示以第i行第j列的格子為右下角，邊長為k的正方形是否符合要求。要想f[i,j,k]=True，首先必須滿足f[i-1,j-1,k-2]為True（灰色部分滿足要求）。另外，我們還需要保證圖中兩塊藍色區域相等，兩塊綠色區域相等，并且這四個區域自身還必須是對稱的。由于動态規劃的狀态已經是三方的了，是以判斷後面的這些條件必須在常數時間裡完成。為此，我們可以在動态規劃前進行以下6個預處理：

以同列不同行的兩個格子(i,j)和(i',j)為右端點，同時向左擴充可以得到多長的相等區域

以同行不同列的兩個格子(i,j)和(i,j')為最底端，同時向上擴充可以得到多長的相等區域

以格子(i,j)為中心，向左右擴充可以得到多長的對稱區域

以格子(i,j)為中心，向上下擴充可以得到多長的對稱區域

以兩個橫向相鄰的格子(i,j-1)和(i,j)為中心，向左右擴充可以得到多長的對稱區域

以兩個縱向相鄰的格子(i-1,j)和(i,j)為中心，向上下擴充可以得到多長的對稱區域

    上面的每個預處理都可以在三方的時間裡完成，動态規劃的決策降到常數級别，是以總的複雜度還是三方。

    同樣地，這也隻是我出這道題的本意。我事先已經想到，這道題應該還有很多其它的算法，隻是沒想到會有那麼多。一個比較容易想到的算法是，執行與上面相同的預處理後，枚舉某個格子（或某個交叉點）為中心，向外一層一層地進行擴充。雖然這樣的複雜度仍然是三方的，并且與前面的算法實質相同，但它的效率顯然更高，因為你可以在無法再向外擴充時停止最裡面的那個循環，繼續枚舉下一個中心點。

    同樣是枚舉正方形的中心點，隻使用上面的後4個預處理也可以解決這個問題。我們可以線上性的時間内找出，以某個格子（或交叉點）為中心的最大的合法正方形。假如這個最大的正方形邊長為k，這相當于我們同時找到了(k+1) div 2個正方形來。至于如何找到這個最大的正方形，還是留給大家思考吧。

    Cockhorse想到了一個非常巧妙的算法，預處理結束後它可以在常數時間内判斷任一個給定的小正方形是否滿足題目要求。用f[i,j,k]表示，以第i行中(i,j)及其右邊相鄰的k-1個格子（共k個格子）來作為底邊，所能得到的左右對稱的矩形其最大高度是多少。則當f[i,j+1,k-2]為True且(i,j)格與(i,j+k-1)格花色相等時f[i,j,k]=f[i-1,j,k]+1（否則f[i,j,k]=0）。同樣地，再用g[i,j,k]表示以(j,i)..(j+k-1,i)作為右邊界，使矩形上下對稱的最大寬度。這樣，判斷任意一個正方形是否滿足題目要求，隻需要檢查它的底邊和右邊能夠産生的最大對稱區域是否可以覆寫該正方形即可。

    當然，這道題目還有很多其它的算法，這裡就不一一列舉了。

Problem 3: 流言的傳播

    給定一個圖，把圖中所有點構成的點集叫做U，另指定一個不等于全集的子集S，那麼所有一個頂點在S裡另一個頂點在U-S裡的邊就叫做S點集的“割邊”，因為去掉所有這樣的邊後S集将孤立出來。這道題就是需要你找出一個邊集E，使得不管S集是什麼，對應的割邊中權值最小的那一條一定在邊集E中。這樣的邊集肯定是存在的，比如所有邊構成的集合就是一個滿足條件的邊集。這道題希望你找到的邊集E裡所含的邊盡可能的少。

    一個錯誤的貪心法是，去掉每個點的鄰接邊中權值最小的那一條。這種算法顯然不對，比如下面就是一個鮮活的反例：

o-----o-----o-----o

   2     3     1

    在上圖中，每個點的鄰接邊中權值最小的不是1就是2，這樣的話中間那條邊就被保留了下來，于是令S集為左邊兩個點（或右邊兩個點），割邊仍然一條不少。很容易想到，要想讓任意S集的割邊中權值最小的被去掉，首先得保證邊集E連通了所有的點，否則令S等于任一連通分量，邊集E裡都不會包含任何一條割邊。這樣，邊集E至少要有n-1條邊。

    考慮到最優解至少是n-1條邊，這n-1條邊必須連通所有的點，而所選邊的權值都應該很小，于是想到最後的答案很可能就是最小生成樹。現在假設我們已經選擇了某些邊，這些邊形成了若幹個連通分量。考慮所有連接配接兩個不同的連通分量的邊（兩頂點不在同一連通分量的邊）中權值最小的一條，那這條邊必須要選，否則令S集為其中一個連通分量，題目條件就不能達到了。這不就是Kruskal算法嗎？

    且慢，我們還沒有證明，對任意一個S集，最小生成樹都符合條件。證明其實很簡單，假設權值最小的割邊e不在最小生成樹E中，添加割邊e将形成一個回路。這條回路将從S集的某個點出發，經過e跑到U-S裡，最後必須還要回到S集。回到S集必然要經過另一條割邊e'，而顯然e'>e（因為e是權值最小的割邊，且題目說了沒有權值相同的邊），于是邊集E+{e}-{e'}就成了更小的生成樹。

Problem 4: 表白機器人

    第四題是整個模拟賽中最簡單的題，它不需要你構造任何算法，你隻需要按照題目意思進行模拟即可。和去年的NOIp一樣，純粹考程式設計能力的題目并沒有放在第一道題的位置上。這提示大家拿到題目後要先看完所有的題，特别是看到最後一道題時千萬别慌，很可能把它的衣服扒光了一看，發現它居然是一道赤裸裸的送分題。

    為了加快速度，先預處理出一個數組wall[i][j][k]，表示第i行第j列往k(1<=k<=4)方向上走是否走得通。然後枚舉所有可能的指令序列，模拟機器人的行走過程，看它是否能到達終點。在模拟過程中，你需要用一個數組hash[i][j][k]表示機器人曾在序列的第k個指令後到達第i行第j列的位置，并在模拟過程中不斷更新hash數組；當某一次指令後機器人還沒走到右上角，而對應的hash值已經為True了，則機器人的行動将從這裡開始循環，永遠也到不了右上角了。

    雖然這道題不需要任何剪枝，但我還想再說一句。這道題有一個非常有趣的剪枝：指令序列的第一個指令隻能是U或R，最後一個指令也隻能是U或R。大家想想這是為什麼。