算法流程
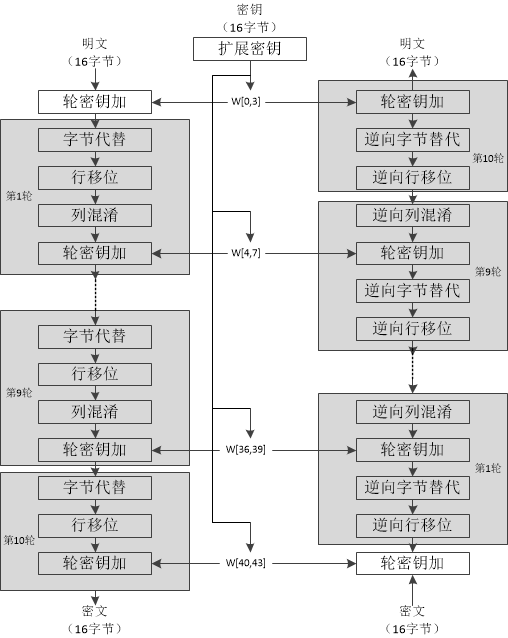
AES加密算法涉及4種操作:位元組替代(SubBytes)、行移位(ShiftRows)、列混淆(MixColumns)和輪密鑰加(AddRoundKey)。下圖給出了AES加解密的流程,從圖中可以看出:1)解密算法的每一步分别對應加密算法的逆操作,2)加解密所有操作的順序正好是相反的。正是由于這幾點(再加上加密算法與解密算法每步的操作互逆)保證了算法的正确性。加解密中每輪的密鑰分别由種子密鑰經過密鑰擴充算法得到。算法中16位元組的明文、密文和輪子密鑰都以一個4x4的矩陣表示。
1.1 位元組替代
位元組代替的主要功能是通過S盒完成一個位元組到另外一個位元組的映射。S盒的詳細構造方法可以參考文獻[4]。這裡直接給出構造好的結果,下圖(a)為S盒,圖(b)為S-1(S盒的逆)。S盒用于提供密碼算法的混淆性。
S和S-1分别為16x16的矩陣,完成一個8比特輸入到8比特輸出的映射,輸入的高4-bit對應的值作為行标,低4-bit對應的值作為列标。假設輸入位元組的值為a=a7a6a5a4a3a2a1a0,則輸出值為S[a7a6a5a4][a3a2a1a0],S-1的變換也同理。
例如:位元組00000000B替換後的值為(S[0][0]=)63H,再通過S-1即可得到替換前的值,(S-1 [6][3]=)00H。
1.2 行移位
行移位是一個4x4的矩陣内部位元組之間的置換,用于提供算法的擴散性。
1) 正向行移位
正向行移位用于加密,其原理圖如下。其中:第一行保持不變,第二行循環左移8比特,第三行循環左移16比特,第四行循環左移24比特。
假設矩陣的名字為state,用公式表示如下:state’[i][j] = state[i][(j+i)%4];其中i、j屬于[0,3]。
2) 逆向行移位
逆向行移位即是相反的操作,即:第一行保持不變,第二行循環右移8比特,第三行循環右移16比特,第四行循環右移24比特。
用公式表示如下:state’[i][j] = state[i][(4+j-i)%4];其中i、j屬于[0,3]。
1.3 列混淆
列混淆:利用GF(28)域上算術特性的一個代替,同樣用于提供算法的擴散性。
1) 正向列混淆
正向列混淆的原理圖如下:
根據矩陣的乘法可知,在列混淆的過程中,每個位元組對應的值隻與該列的4個值有關系。此處的乘法和加法都是定義在GF(28)上的,需要注意如下幾點:
1) 将某個位元組所對應的值乘以2,其結果就是将該值的二進制位左移一位,如果原始值的最高位為1,則還需要将移位後的結果異或00011011;[1]
英文原文描述如下:In particular, multiplication of a value by x (i.e., by {02}) can be implemented as a 1-bit left shift followed by a conditional bitwise XOR with (0001 1011) if the leftmost bit of the original value (prior to the shift) is 1.
2) 乘法對加法滿足配置設定率,例如:07·S0,0=(01⊕02⊕04)·S0,0= S0,0⊕(02·S0,0)(04·S0,0)
3) 此處的矩陣乘法與一般意義上矩陣的乘法有所不同,各個值在相加時使用的是模28加法(異或運算)。
下面舉一個例子,假設某一列的值如下圖,運算過程如下:
在計算02與C9的乘積時,由于C9對應最左邊的比特為1,是以需要将C9左移一位後的值與(0001 1011)求異或。同理可以求出另外幾個值。
2) 逆向列混淆
逆向列混淆的原理圖如下:
由于:
說明兩個矩陣互逆,經過一次逆向列混淆後即可恢複原文。
1.4 輪密鑰加
這個操作相對簡單,其依據的原理是“任何數和自身的異或結果為0”。加密過程中,每輪的輸入與輪子密鑰異或一次;是以,解密時再異或上該輪的輪子密鑰即可恢複。
1.5 密鑰擴充算法
密鑰擴充的原理圖如下:
密鑰擴充過程說明:
1) 将種子密鑰按圖(a)的格式排列,其中k0、k1、……、k15依次表示種子密鑰的一個位元組;排列後用4個32比特的字表示,分别記為w[0]、w[1]、w[2]、w[3];
2) 按照如下方式,依次求解w[j],其中j是整數并且屬于[4,43];
3) 若j%4=0,則w[j]=w[j-4]⊕g(w[j-1]),否則w[j]=w[j-4]⊕w[j-1];
函數g的流程說明:
a) 将w循環左移8比特;
b) 分别對每個位元組做S盒置換;
c) 與32比特的常量(RC[j/4],0,0,0)進行異或,RC是一個一維數組,其值如下。(RC的值隻需要有10個,而此處用了11個,實際上RC[0]在運算中沒有用到,增加RC[0]是為了便于程式中用數組表示。由于j的最小取值是4,j/4的最小取值則是1,是以不會産生錯誤。)
RC = {0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36}
1.6 小結
密碼算法要求是可逆的,這樣解密算法才能正确的恢複明文。拿AES來說,在密鑰固定的情況下,明文和密文在整個輸入空間是一一對應的。是以算法的各個部件也都是可逆的,再将各個部件的操作順序設計成可逆的,密文就能正确的解密了。
參考網址:https://www.cnblogs.com/luop/p/4334160.html
github連結:https://github.com/allenlee820202/Parallel-AES-Algorithm-using-CUDA