2225. [SDOI2016 Round1] 征途
★★★☆ 輸入檔案:
menci_journey.in
輸出檔案:
menci_journey.out
簡單對比
時間限制:1 s 記憶體限制:256 MB
【題目描述】
Pine 開始了從 S 地到 T 地的征途。
從 S 地到 T 地的路可以劃分成 n 段,相鄰兩段路的分界點設有休息站。
Pine 計劃用 m 天到達 T 地。除第 m 天外,每一天晚上 Pine 都必須在休息站過夜。是以,一段路必須在同一天中走完。
Pine 希望每一天走的路長度盡可能相近,是以他希望每一天走的路的長度的方差盡可能小。
幫助 Pine 求出最小方差是多少。
設方差是 v,可以證明,v×m2 是一個整數。為了避免精度誤差,輸出結果時輸出 v×m2。
【輸入格式】
第一行兩個數 n、m。
第二行 n 個數,表示 n 段路的長度。
【輸出格式】
一個數,最小方差乘以 m2 後的值。
【樣例輸入】
5 2
1 2 5 8 6
【樣例輸出】
36
【提示】
對于 30% 的資料,1≤n≤10。
對于 60% 的資料,1≤n≤100。
對于 100% 的資料,1≤n≤3000。
保證從 S 到 T 的總路程不超過 30000。
【來源】
SDOI2016 Round1 Day2
資料已由出題人修正
我們把f[i][j]作為用過了第i次一共取了j個數的最小值.
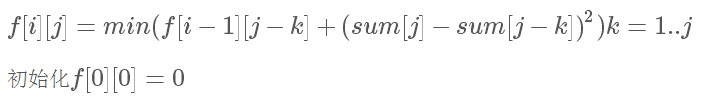
斜率優化:
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
#define pf(x) ((x)*(x))
#define FRE(name) freopen(#name".in","r",stdin);freopen(#name".out","w",stdout);
#ifdef WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
const int N=3005;
int n,m,a[N],q[N];
ll ans,sum[N],f[N][N];
inline double get(int i,int x,int y){
return ((double)(f[i][x]-f[i][y]+pf(sum[x])-pf(sum[y])))/((double)(sum[x]-sum[y]));
}
int main(){
FRE(menci_journey);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
memset(f,0x3f3f3f3f,sizeof f);
f[0][0]=0;
for(int i=1;i<=m;i++){
int h=1,t=1;
for(int j=1;j<=n;j++){
while(h<t&&get(i-1,q[h+1],q[h])<(double)(sum[j]<<1)) h++;//擷取目前最優k
f[i][j]=f[i-1][q[h]]+pf(sum[j]-sum[q[h]]);
while(h<t&&get(i-1,q[t],q[t-1])>get(i-1,j,q[t])) t--;//維護min(slope)
q[++t]=j;
}
}
ans=f[m][n]*m-pf(sum[n]);
printf(LL,ans);
return 0;
} 轉載于:https://www.cnblogs.com/shenben/p/6625503.html