問題提出
工業生産活動的目标是利用原料生産産品,進而産生利潤。原料經過一系列加工過程,包括實體反應和化學反應,最終形成産品,生産的理想狀态是原料到産品的轉換率是确定的,工廠想生産多少産品就知道需要準備多少原料,提高生産效率。
許多工藝原理和生産經驗都表明,在簡化情況下,可以認為原料用量和産品産量之間近似是線性關系。這樣,每一種原料和每一種産品之間都會有一個與原料用量無關的恒定轉換率,在化工界稱為收率。
我們的目标是根據曆史的原料量和産量計算出一個較準确的收率,然後在下一個生産周期(比如第二天)中根據原料用量預測産量,預測産量與實際産量越接近說明收率越準确。如下圖:
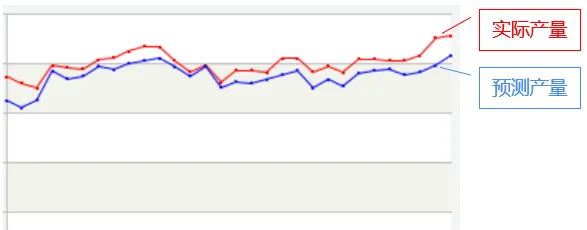
反應在圖上,目标就是使兩條曲線盡可能重合。
怎麼才能算出一個較準确的收率呢?
既然原料用量和産品産量之間近似是線性關系,而線性拟合又是非常成熟的技術,那麼很容易想到,直接用曆史資料進行線性拟合就可以解決問題了。
可是,現實情況并沒有這麼簡單,由于資料的各種測量誤差,直接使用線性拟合算法會得出非常荒唐的結果:
- 收率大于1,這意味着産品産量大于原料用量,憑空造出很多産品;
- 收率小于0,這更加離譜,原料越多反而産量越少。
這兩種情況顯然都違背了品質守恒定律,在現實場景中是不可能發生的,這樣拟合出來的收率也沒有任何用于預測的意義。
如此看來,原料和産品的拟合并不是完全無條件的,需要滿足品質守恒定律,即所有産品産量小于原料用量且不會因原料增多而減少,這要求所有收率必須在[0,1]範圍内。
品質守恒定律還要求任一種原料最終都轉化成各種産品,不會有沒有用掉的原料,也不會憑空産生産品,即各種産品對某一種原料的收率和等于1。
正常的線性拟合算法,隻考慮拟合結果與目标最接近,并不考慮這些限制,是以當原始資料有誤差時,拟合出荒唐的結果也就不奇怪了。
此外,工藝知識還提供了基礎收率,它是個長期均值,直接用它預測“明天” 的産品産量效果很差,好比用年均氣溫去預測明天氣溫,顯然無效,是以基礎收率不能直接使用,隻能作為參考,就像預測“明天”氣溫可以把年均氣溫作為參考一樣,不能偏離特别遠,否則即使拟合結果誤差很小也不合适用于預測。
綜上所述,限制條件有3個,分别是:
限制1:所有收率都在[0,1]範圍内。
限制2:各種産品對某一種原料的收率和等于1。
限制3:不可以偏離基礎收率太遠。
我們的任務是研究如何在這些限制條件下利用原料和産品資料計算出較準确的收率,使其可以用于預測第二天的産量。
算法思路
利用曆史資料,考慮用不同的數學方法來滿足3個限制條件:
- 有邊界的線性拟合法來滿足限制1
我們可以把0和1作為邊界,問題就轉化成有邊界的線性拟合,最優解一定會在邊界或者是線性拟合結果處。把問題簡單化以後就是我們中學時期解的二進制一次函數在指定範圍内的最大或最小值問題,如下圖:
所幸實際生産中原料的種類不會特别多,窮舉所有這些情況,最後找到誤差最小的解即可滿足收率範圍在[0,1]内這一限制條件。
- 線性變換方法來滿足限制2。
n種産品的收率和為1,意味着這些收率線性相關。有邊界的拟合方法不能保證收率和不為1,可以将誤差按權重線性分拆到各産品上修正收率,反複疊代即可滿足收率和為1這一限制條件。如下圖:
- 拟合偏差的方法來滿足限制3。
今天的氣溫和明天差别不大,可以把今天和一年的平均氣溫之差作為計算明天氣溫的參考,如下圖:
同理,實際生産中,收率同氣溫一樣也是漸變的,即今天的收率和明天的收率差别不會很大,可以把今天的收率和基準收率得到的産品産量之差作為計算明天收率的參考,以此作為有邊界拟合時的邊界,保證結果收率不偏離基礎收率太遠。如下圖:
這樣得到的收率就可以同時滿足三個限制條件,而且準确性也高于基礎收率。
實踐效果
把上面思路寫成代碼,就可以計算收率了。
| A | |
| 1 | [[30,8],[31,7],[38,10]] |
| 2 | [[2,13,23],[3,15,20],[11,13,24]] |
| 3 | [[0,0.5,0.5],[0.55,0.05,0.4]] |
| 4 | 0.1 |
| 5 | =mul(A1,A3) |
| 6 | =A2.(~--A5(#)) |
| 7 | =bd(A1,A2,A3,A4).(~.(~.(round(~,3)))) |
| 8 | =A6.~.((idx=#,bdfit(A1,A6.([~(idx)]),A7.(~(idx))).conj())) |
| 9 | =transpose(A8) |
| 10 | =func(A12,A9,A3) |
SPL提供了很多矩陣計算方法,可以高效的進行矩陣運算,搭配其強大的集合運算能力,可以高效的實作上述算法思路。
計算結果示例:
原料X:
産品Y:
基礎收率B:
最終的收率W:
下面是直接用最小二乘法拟合得到的收率W’:
很顯然,它的結果有的大于1,有的小于0,完全不滿足限制條件,是以無法使用。
通過驗證,W滿足3個限制條件,為了進一步驗證W的準确性,我們用它和基礎收率B對比,以均方誤差MSE作為評價标準,MSE越小,預測産品産量與實際産量差距越小,收率越準确。
先來看使用基礎收率B,各出料的均方誤差MSE:
MSE1=12.24
MSE2=16.24
MSE3=8.98
其中MSEj是第j個出料的MSE。
再看使用W,各出料的MSE:
MSE1=10.97
MSE2=5.13
MSE3=3.86
很明顯,拟合後的W效果更好。
最後說明一下,本文隻介紹優化産品收率的思路,具體的計算過程并沒有較長的描述。文中的代碼也是示意性的,因為有邊界的線性拟合、計算邊界範圍、線性變換等都需要大量的運算,都展示出來隻會使文章變的臃腫且晦澀難懂,如果有讀者對細節過程感興趣,可以和我們聯系溝通。
資料
- SPL下載下傳
- SPL源代碼