注:本文中所有公式和思路來自于鄒博先生的《機器學習更新版》,我隻是為了加深記憶和了解寫的本文。
這次要分享的是模型是條件随機場模型,聽起來就是不是十分的容易,不過也确實是這樣子的,學習條件随機場之前個人覺得最好先學習HMM模型,因為條件随機場和HMM有很多共同的地方,比方說都是機率圖模型、最基本的三個問題也是一模一樣的(機率計算、學習問題、預測問題)。
這裡先給出一個條件随機場的定義:條件随機場時給定一組輸入随機變量X的條件下另一組随機變量Y的條件機率分布模型,其特點是假設輸出随機變量Y構成馬爾科夫随機場。大家一定記得Logistic吧,Logistic這個模型中不也是給定輸入随機變量X的條件下另一組随機變量Y的條件機率麼,隻不過Logistic的輸出随機變量時離散的、互相之間是獨立的,而CRF(條件随機場)的輸出随機變量之間我們是假設構成馬爾科夫随機場的,僅此而已,是以我們可以套用Logistic的套路來搞點事情。
那麼什麼是馬爾科夫随機場呢?
機率無向圖模型:設有聯合機率分布p(Y),由無向圖G=(V,E)表示,在圖G中,V(結點)表示随機變量,E(邊)表示随機變量之間的依賴關系,如果聯合機率P(Y)滿足成對、局部、全局馬爾科夫性,就稱此聯合機率分布為機率無向圖模型(probability undirected graphical model),或馬爾科夫随機場(Markov random filed)
那麼什麼是成對、局部、全局馬爾科夫性呢?
我隻說一下局部和全局馬爾科夫性,成對的極其簡單,和局部、全局都是一個道理。
局部馬爾科夫性:
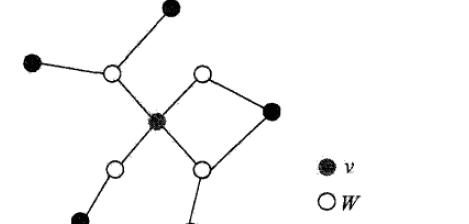
稍作解釋:圖中分為三部分v、w、o,如果給定w,那麼v和o就是獨立的,公式化的解釋是:
全局馬爾科夫性:
解釋:給定三個集合A、B、C,如果給定C集合,那麼A、B兩個集合就是條件獨立的,公式化解釋:
成對、局部、全局馬爾科夫性是等價的,後兩個是成對馬爾科夫性推廣而來的。此處文獻可以查閱李航博士的《統計學習方法》。
條件随機場有多種形式,本文隻介紹線性鍊條件随機場,也就是說輸出随機變量是在一條鍊上的,我們可以這麼來了解。
下面這種是我們最常見的一種線性鍊條件随機場
從Logistic談起
假定:
則有:
對數似然:
對參數求導:
Logistic回歸的參數學習過程:
我們都知道一件事情發生的幾率是該事件發生的機率與不發生機率的比值,那麼對數幾率就可以這麼寫:
那麼對數線性模型的一般形式可以這麼寫:
其中我們将Logistic/Softmax回歸的特征記作Fj(x, y),歸一化因子為:
給定一個x的預測标記為:
當然了,CRF畢竟跟Logistic有很大的不同,但是思考的思路我們不妨借鑒一下Logistic。
線性鍊條件随機場可以使用對數線性模型來做,使用
來表示n個詞的序列,使用
表示相應的詞性:
畢竟和Logistic不同,我們定義
的第j個特征Fj是有若幹的次特征組成:
這裡fj依賴或者部分依賴于目前的整個句子
、目前的詞的标記yi、前一個詞的标記yi-1,目前詞在句子中的位置i:
那麼我們接下來就要找出參數,滿足下式的w,即為最終所求參數:
我們進一步将前邊的公式帶入:
這裡是省略了歸一化因子和指數e,因為對我們求最值來說沒影響,是以簡化了一下,進一步代入公式:
其中第一行第二個等号隻不過是将加和和w換了位置,不影響結果,第二行是将兩個加和互換位置,也不會對結果有影響,最後一行是做了一個定義,也就是g函數,其實這塊有一處有問題,應該是gi而不是gj,因為關于i的一個函數,其實無關緊要,接着往下來。
接着我們令αk(v)為前向得分,表示第k個詞的标記為v的最大的分(歸一化後為機率):
這塊其實我們在别的資料上被介紹為t和s函數,其實是一樣的,gi或者說s是關于邊的轉移特征函數,gk或者t是關于結點的狀态特征函數,那麼我們的遞推公式為:
時間複雜度是O(m^2n),其中标記數為m,句子中包含的單詞數目為n。
那該怎麼計算機率呢?
由于:
得:
從最後一步公式中,我們可以看出,實作對一堆東西算乘積再加和,這不就矩陣乘法嘛,是以我們定義一個m*m得矩陣:
那麼對于M1,我們任選一個u=start,Mn+1任選一個v=stop,那麼從M1到M2可以如下表示:
推廣到n+1:
那麼現在回到之前的求參數得問題上,我們是要求出權向量w,使得下面得式子成立:
我們可以對其取對數,然後求駐點:
計算梯度:
這個求導得過程我就不一步步細講了,其中" ' "和" " "隻是标記而已,不是二階導數,那麼我們就可得到梯度上升得公式:
其中α是學習率。
至此CRF中的機率計算問題就完全說完了,當然還有兩外兩個問題就是學習問題和預測問題,這兩個問題請看我得HMM幾篇文章中得幾個算法,都是可以解決的。
歡迎批評指正!!