餘弦距離的應用 -- cosine distance

在機器學習問題中，通常将特征表示為向量的形式，是以在分析兩個特征向量之間的相似性時，常使用餘弦相似度來表示，其取值範圍為[ -1, 1 ]。

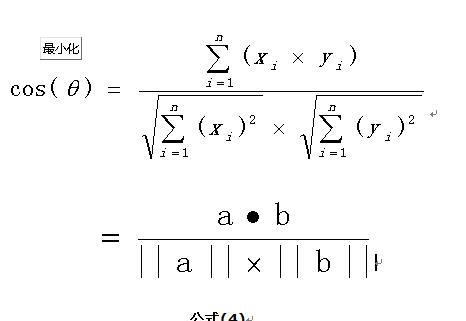
如果希望得到類似于距離的表示，餘弦距離 = 1 - 餘弦相似度，其取值範圍為[ 0， 2 ]，即相同的兩個向量餘弦距離為0。

當一對文本相似度的長度差距很大、但内容相近時，如果使用詞頻或者詞向量作為特征，它們在特征空間中的歐氏距離通常很大；而如果使用餘弦相似度的話，它們之間的夾角可能很小，因而相似度高。

此外，在文本、圖像、視訊等領域，研究的對象的特征次元往往很高，餘弦相似度在高維情況下依然保持“相同時為1，正交時為0，相反時為-1”的性質，而歐氏距離的數值則受次元的影響，範圍不固定，并且含義比較模糊。

總體來說，歐氏距離展現數值上的絕對差異，而餘弦距離展現方向上的相對差異。

注意：餘弦距離不是嚴格定義上的距離！

一般嚴格定義的距離需滿足三條公理：正定性 { 即dist(a,b)>=0 }，對稱性 { dist(a,b) = dist(b, a) }，三角不等式 { 三點中任意兩點的“距離”和都得大于等于剩餘兩點的距離，其中等号在三點“共線”時成立，這裡的“距離” 是這裡用到的度量}

餘弦距離 不滿足 三角不等式。反例：A( 1, 0 )，B( 1, 1 )，C(0, 1)

此外，相對熵 Relative Entropy  也叫 KL散度 也不是嚴格定義上的距離，不滿足 對稱性 和 三角不等式

對稱性是顯然的，基本上随便的測時資料都不滿足對稱性，三角不等式 的證明此處略過，可自行查新相關資料。

KL簡單介紹 ： https://blog.csdn.net/m0_38024592/article/details/100069931